题目内容
若一个三角形三边的长均满足方程x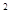
－4x＋3=0，则此三角形的周长是 。
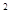－4x＋3=0，则此三角形的周长是 。
先解一元二次方程，由于未说明两根哪个是三角形的边长，故需分情况讨论，从而得到其周长．
解：原方程可化为：（x-3）（x-1）=0，
解得x=3或x=1；
①当三角形的三边长均为3时，此三角形的周长为3+3+3=9；
②当三角形的三边长均为1时，此三角形的周长为1+1+1=3；
③当三角形其中一边为1，另两边为3时，3-1＜3＜3+1，能构成三角形，其周长为3+3+1=7；
④当三角形其中一边为3，另两边为1时，1+1＜3，构不成三角形，故此种情况不成立．
所以此三角形的周长是3或7或9．
解：原方程可化为：（x-3）（x-1）=0，
解得x=3或x=1；
①当三角形的三边长均为3时，此三角形的周长为3+3+3=9；
②当三角形的三边长均为1时，此三角形的周长为1+1+1=3；
③当三角形其中一边为1，另两边为3时，3-1＜3＜3+1，能构成三角形，其周长为3+3+1=7；
④当三角形其中一边为3，另两边为1时，1+1＜3，构不成三角形，故此种情况不成立．
所以此三角形的周长是3或7或9．
练习册系列答案
金钥匙试卷系列答案
相关题目
的一元二次方程
的一个根是2．
的值和方程的另一个根
=16； 
．
的两根分别为【 】
，则
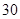场，共有 个队参加比赛。