Question

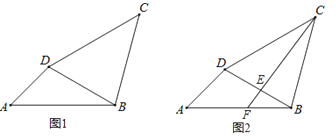
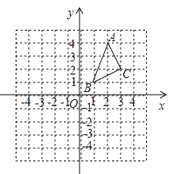
【题目】如图，△ABC中，∠BAC=90°，AB=AC，AD⊥BC于D，AE平分∠BAD，交BC于E，在△ABC外有一点F，使FA⊥AE，FC⊥BC．
（1）求证：BE=CF；
（2）在AB上取一点M，使得BM=2DE，连接ME
①求证：ME⊥BC；
②求∠EMC的度数．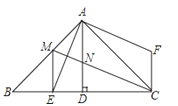

Answer 1

【答案】证明：（1）∵△ABC中，∠BAC=90°，AB=AC，
∴∠ABC=∠ACB=45°，
∵FC⊥BC，
∴∠ACF+∠ACB=90°，
∴∠ACF=45°=∠ABE．
∵∠BAC=90°，FA⊥AE，
∴∠BAE+∠EAC=90°=∠CAF+∠EAC，
∴∠BAE=∠CAF．
在△ABE和△ACF中，，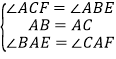
∴△ABE≌△ACF（ASA），
∴BE=CF．
（2）①证明：过点E作EQ⊥AB于点Q，如图所示．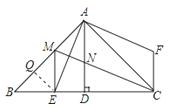

∵AE平分∠BAD，
∴∠QAE=∠DAE，
在△AEQ和△AED中，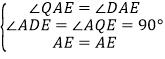
∴△AEQ≌△AED（AAS），
∴QE=DE．
∵∠BQE=90°，∠QBE=45°，
∴∠BEQ=45°，
∴BQ=QE，
又∵BM=2DE=QE，
∴QM=QE，
∴∠QEM=∠QME==45°，
∴∠BEM=∠BEQ+∠QEM=90°，
∴ME⊥BC．
②解：设DE=a，则BM=2a．
∵△BEM为等腰直角三角形，
∴BE=EM=BM=a，
∴BD=BE+DE=（+1）a．
∵△ABC为等腰直角三角形，AD⊥BC，
∴AB=BD=×（+1）a=（2+）a，
∵BM=2a，
∴AM=（2+）a﹣2a=a，
∴AM=EM．
在Rt△MAC和Rt△MEC中，，
∴Rt△MAC≌Rt△MEC（HL），
∴∠EMC=∠AMC，
又∵∠BME=45°，
∴∠EMC=（180°﹣45°）=67.5°．
【解析】（1）由等腰直角三角形的性质可知∠ABC=∠ACB=45°，由FC⊥BC可知∠ACF=45°，从而得出∠ABE=∠ACF；由∠BAE、∠CAF均为∠EAC的余角可得出∠BAE=∠CAF，结合AB=AC即可得出△ABE≌△ACF，根据全等三角形的性质即可得出结论；
（2）①过点E作EQ⊥AB于点Q，由△AEQ≌△AED可得出QE=DE；根据∠BQE=90°和∠QBE=45°可得出∠BEQ=45°、BQ=QE，再由BE=2DE=2QE即可得出∠QEC=45°，由此可得出∠BEM=90°，即ME⊥BC；②设DE=a，则BM=2a，根据等腰直角三角形的性质可用含a的代数式表示AB和BD，由边与边的关系可得出AM=ME，结合MC=MC可证得Rt△MAC≌Rt△MEC，即∠EMC=∠AMC，再根据角与角的关系即可得出结论．
【考点精析】利用等腰直角三角形对题目进行判断即可得到答案，需要熟知等腰直角三角形是两条直角边相等的直角三角形；等腰直角三角形的两个底角相等且等于45°．