题目内容
【题目】如图![]() ,已知在四边形
,已知在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() 平分
平分![]() ,交
,交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,
,![]() 是
是![]() 的中点,连接
的中点,连接![]() ,
,![]() ,
,![]() .
.

![]() 求证:四边形
求证:四边形![]() 是菱形;
是菱形;
![]() 若
若![]() ,如图
,如图![]() 所示:
所示:
①求证:![]() ;
;
②若![]() ,求
,求![]() 的度数.
的度数.
【答案】(1)证明见解析(2)见解析
【解析】
(1)根据平行四边形的性质得出AD∥BC,求出四边形ABFE是平行四边形,求出AB=AE,根据菱形的判定得出即可;
(2)①过O作ON∥BC交DC于N,根据矩形的判定得出四边形ABCD是矩形,根据矩形的性质得出∠ADC=∠BCD=90°,AD∥BC,求出N为DC的中点,ON⊥DC,根据线段垂直平分线性质得出OD=OC,即可得出答案;
②根据正方形的判定得出四边形ABFE是正方形,根据正方形的性质得出∠AEB=45°,根据三角形外角性质求出∠EDO=30°,求出∠ODC即可.
![]() 证明:∵四边形
证明:∵四边形![]() 是平行四边形,
是平行四边形,
∴![]() ,即
,即![]() ,
,
∵![]() ,
,
∴四边形![]() 是平行四边形,
是平行四边形,
∵![]() ,
,
∴![]() ,
,
∵![]() 平分
平分![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴平行四边形![]() 是菱形;
是菱形;
![]() ①过
①过![]() 作
作![]() 交
交![]() 于
于![]() ,
,
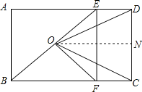
∵![]() ,
,![]() ,
,![]() ,
,
∴四边形![]() 是矩形,
是矩形,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() 为
为![]() 的中点,
的中点,
∴![]() 为
为![]() 的中点,
的中点,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ;
;
②解:∵四边形![]() 是平行四边形,
是平行四边形,![]() ,
,![]() ,
,
∴四边形![]() 是正方形,
是正方形,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() .
.

练习册系列答案
相关题目






