题目内容
如图,Rt△ABC中,∠ACB=90°,AC=4,BA=5.P是AC上的动点(P不与A、C重合),设P C=x,点P到AB的距离为y.
C=x,点P到AB的距离为y.
(1)求y与x的函数关系式;
(2)试讨论以P为圆心,半径长为x的圆与AB所在直线的位置关系,并指出相应的x的取值范围.
解:(1)根据勾股定理得BC=3.
用面积关系S△ABC=S△PBC+S△APB,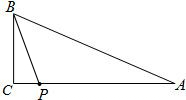
即 x+
x+ y=6,
y=6,
y= (0<x<4).
(0<x<4).
(2)当x=y,
则x=- x+
x+ ,
,
解得:x= .
.
∴当0<x< 时,圆P与AB所在直线相交;
时,圆P与AB所在直线相交;
当x= 时,圆P与AB所在直线相切;
时,圆P与AB所在直线相切;
当 <x<4时,圆P与AB所在直线相离.
<x<4时,圆P与AB所在直线相离.
分析:(1)根据大直角三角形的面积=两个三角形的面积和进行推导;
(2)根据不同的位置关系应满足的数量关系进行分析讨论.
点评:能够根据不同的方法表示同一个图形的面积建立函数关系式;根据不同的位置关系应满足的数量关系列不等式求解.
用面积关系S△ABC=S△PBC+S△APB,

即
 x+
x+ y=6,
y=6,y=
 (0<x<4).
(0<x<4).(2)当x=y,
则x=-
 x+
x+ ,
,解得:x=
 .
.∴当0<x<
 时,圆P与AB所在直线相交;
时,圆P与AB所在直线相交;当x=
 时,圆P与AB所在直线相切;
时,圆P与AB所在直线相切;当
 <x<4时,圆P与AB所在直线相离.
<x<4时,圆P与AB所在直线相离.分析:(1)根据大直角三角形的面积=两个三角形的面积和进行推导;
(2)根据不同的位置关系应满足的数量关系进行分析讨论.
点评:能够根据不同的方法表示同一个图形的面积建立函数关系式;根据不同的位置关系应满足的数量关系列不等式求解.

练习册系列答案
相关题目

 如图,Rt△ABC中,∠ACB=90°,tanB=
如图,Rt△ABC中,∠ACB=90°,tanB= 如图,Rt△ABC中,∠C=90°,BC=3,AC=4,若△ABC∽△BDC,则CD=( )
如图,Rt△ABC中,∠C=90°,BC=3,AC=4,若△ABC∽△BDC,则CD=( ) 如图,Rt△ABC中,∠C=90°,△ABC的内切圆⊙0与BC、CA、AB分别切于点D、E、F.
如图,Rt△ABC中,∠C=90°,△ABC的内切圆⊙0与BC、CA、AB分别切于点D、E、F. 如图,Rt△ABC中,∠ABC=90゜,BD⊥AC于D,∠CBD=α,AB=3,BC=4.
如图,Rt△ABC中,∠ABC=90゜,BD⊥AC于D,∠CBD=α,AB=3,BC=4.