Question

【题目】[感知] 如图①，在四边形ABCD中，点P在边AB上（点P不与A、B重合）， ， 易证： △DAP∽△PBC（不要求证明）

[探究]如图②，在四边形ABCD中，点P在边AB上（点P不与A、B重合），

（1）求证：△DAP∽△PBC.

（2）若PD=5，PC=10.BC=8求AP的长.

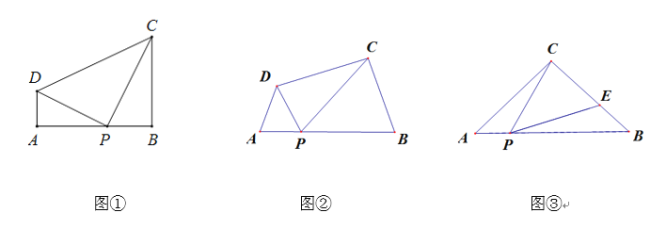
[应用]如图③，在△ABC中，AC=BC=4，AB=6，点P在边AB上（点P不与A、B重合），连结CP，作 ，与边BC交于点E.当CE=3EB时，直接写出AP的长.

Answer 1

【答案】（1）详见解析；（2）4；[应用]AP=

【解析】

（1）由三角形外角性质可得∠DPB=∠A+∠ADP，然后推出∠ADP=∠CPB即可证明相似；

（2）由相似得到对应边成比例，建立方程即可求AP；

[应用]同（1）的方法，先证明∠EPB=∠ACP，然后证明△APC∽△BEP，再由对应边成比例建立方程求AP.

（1）∵∠DPB=∠A+∠ADP，

∴∠DPC+∠CPB=∠A+∠ADP，

∵∠A=∠DPC，

∴∠ADP=∠CPB

∵∠A=∠B

∴

（2）

∴

∴

∴AP=4.

[应用]AP=，理由如下：

∵∠BPC=∠A+∠ACP

∴∠CPE+∠EPB=∠A+∠ACP

∵∠CPE=∠A

∴∠EPB=∠ACP

又∵AC=BC

∴∠A=∠B

∴△APC∽△BEP

∴

∵CE=3EB

∴BE=BC=1

∴

解得AP=