Question

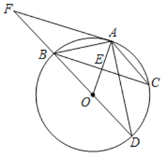
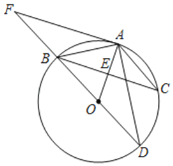
【题目】如图，BD是⊙O的直径，弦BC与OA相交于点E，AF与⊙O相切于点A，交DB的延长线于点F，∠F＝30°，∠BAC＝120°，BC＝8．

（1）求∠ADB的度数；

（2）求AC的长度．

Answer 1

【答案】（1）30°；（2）

【解析】

（1）根据切线的性质可得：AF⊥OA，结合已知条件和三角形内角和定理即可求出∠BOA，根据圆周角定理即可求出∠ADB；

（2）根据直径所对的圆周角是直角可得：∠BAD=90°，从而求出∠DBC=∠DAC=30°，根据平行线的判定及性质可得：OA⊥BC，然后根据垂径定理可得：BE＝CE＝BC＝4，再根据垂直平分线的性质可得：AB＝AC，利用等边三角形的判定证出：△AOB是等边三角形，可得：OB=AB＝AC，然后根据锐角三角函数可求出BE，从而求出AC.

解：（1）∵AF与⊙O相切于点A，

∴AF⊥OA，

∴∠OAF=90°

∵∠F=30°

∴∠BOA＝180°﹣∠OAF﹣∠F＝60°，

∴∠ADB＝∠AOB＝30°；

（2）∵BD是直径

∴∠BAD=90°

∵∠BAC＝120°

∴∠DAC=∠BAC－∠BAD=30°

∴∠DBC=∠DAC=30°

∵∠F=30°

∴BC∥FA

∴OA⊥BC，

∴BE＝CE＝BC＝4，

∴AB＝AC，

∵∠AOB＝60°，OA＝OB，

∴△AOB是等边三角形，

∴AB＝OB，

∵∠OBE＝30°，

∴OB＝＝，

∴AC＝AB＝OB＝．