题目内容
【题目】(问题提出)
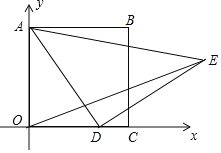
如图①,在![]() 中,若
中,若![]() ,
,![]() ,求
,求![]() 边上的中线
边上的中线![]() 的取值范围.
的取值范围.
(1)(问题解决)
解决此问题可以用如下方法:延长![]() 到点
到点![]() 使
使![]() ,再连接
,再连接![]() (或将
(或将![]() 绕着点
绕着点![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() ),把
),把![]() 、
、![]() 、
、![]() 集中在
集中在![]() 中,利用三角形三边的关系即可判断,由此得出中线
中,利用三角形三边的关系即可判断,由此得出中线![]() 的取值范围.
的取值范围.
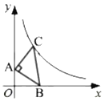
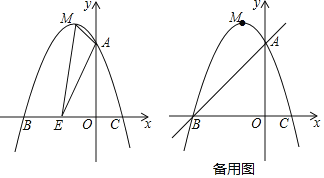
(2)(应用)
如图②,在![]() 中,
中,![]() 为
为![]() 的中点,已知
的中点,已知![]() ,
,![]() ,
,![]() ,求
,求![]() 的长.
的长.
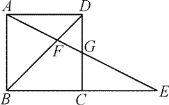
(3)(拓展)
如图③,在![]() 中,
中,![]() ,点
,点![]() 是边
是边![]() 的中点,点
的中点,点![]() 在边
在边![]() 上,过点
上,过点![]() 作
作![]() 交边
交边![]() 于点
于点![]() ,连接
,连接![]() 。已知
。已知![]() ,
,![]() ,求
,求![]() 的长.
的长.

【答案】(1)![]() ;(2)
;(2) ![]() ;(3)
;(3)![]() .
.
【解析】
(1)延长AD到E,使AD=DE,连接BE,证△ADC≌△EDB,推出EB=AC,根据三角形的三边关系求出即可;
(2)同(1)可证△ADC≌△EDB,可得△ABE的三边长,利用勾股定理的逆定理得出△ABE为直角三角形,然后在Rt△BED中利用勾股定理求出BD的长,进而得出BC的长;
(3)延长ED到点G,使DG=ED,连接CG,FG.由△EBD≌△GCD可得∠B=∠GCD、BE=CG=4,根据∠A=90°知∠GCF=90°,利用勾股定理求得FG的长,最后由中垂线性质即可得EF=FG.
(1)解:延长AD到E,使AD=DE,连接BE,
∵AD是△ABC的中线,
∴BD=CD,
在△ADC与△EDB中,
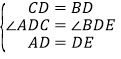 ,
,
∴△ADC≌△EDB(SAS),
∴EB=AC,
根据三角形的三边关系得:AB-AC<AE<AC+AB,
∴2<AE<10,
∵AE=2AD,
∴,1<AD<5,
即:BC边上的中线AD的取值范围1<AD<5;
(2)
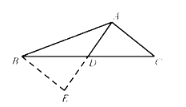
延长AD至E,使DE=AD,连接BE.
∵点D为边BC的中点,
∴BD=CD.
∵∠BDE=∠ADC,
∴△ADC≌△EDB.
∴BE=AC=3,DE=AD=2.
∴AE=4.
∵AB=5,且![]() ,
,
∴![]() .
.
∴△ABE为直角三角形,∠AEB=90°.
∵在Rt△BDE中,∠BED=90°,
∴BD=![]() ,
,
∴BC=2BD=![]() ;
;
(3)

延长ED到点G,使DG=ED,连接CG,FG.
同前法可得△EBD≌△GCD,
∴∠B=∠GCD,BE=CG=4,
又∵∠A=90°,
∴∠B+∠BCA=90°,
∴∠GCD+∠BCA=90°,即∠GCF=90°,
∵CG=4,CF=5,
∴FG=![]() =
=![]() =
=![]() .
.
∴EF= FG =![]() .
.