题目内容
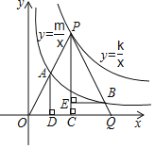
【题目】如图,在第一象限内,动点P在反比例函数y=![]() 的图象上,以P为顶点的等腰△OPQ,两腰OP、PQ分别交反比例函数y=
的图象上,以P为顶点的等腰△OPQ,两腰OP、PQ分别交反比例函数y=![]() 的图象于A、B两点,作PC⊥OQ于C,BE⊥PC于E,AD⊥OQ于D,则以下说选正确的个数为( )个
的图象于A、B两点,作PC⊥OQ于C,BE⊥PC于E,AD⊥OQ于D,则以下说选正确的个数为( )个
①![]() 为定值;②若k=4m,则A为OP中点;③S△PEB=
为定值;②若k=4m,则A为OP中点;③S△PEB=![]() ;④OA2+PB2=PQ2.
;④OA2+PB2=PQ2.
A.4B.3C.2D.1
【答案】A
【解析】
根据反比例函数系数k的几何意义和等腰三角形的性质,相似三角形的性质即可判断.
解:①正确.∵A在反比例函数![]() 的图象上,P在反比例函数
的图象上,P在反比例函数![]() 的图象上,
的图象上,
∴S△AOD=![]() |m|,S△poc=
|m|,S△poc=![]() |k|,
|k|,
∵PC⊥OQ于点C,AD⊥OQ于点D,
∴AD∥PC,
∴△AOD∽△POC,
∴ 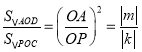 ,
,
∴ ![]() 为定值,
为定值,
∵△OPQ是以P为顶点的等腰三角形,
∴OP=PQ,
∴![]() 为定值;故此选项正确; ②正确,
为定值;故此选项正确; ②正确,
∵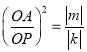 ,k=4m,
,k=4m,
∴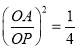 ,
,
∴ ![]() ,故此选项正确;
,故此选项正确;
③正确,延长BE交OP于F,交y轴于M,作BN⊥x轴于N,易证得△OMF≌△BNQ, ∴S四边形OMBN=S四边形OFBQ=m, 即可证得S四边形CQBE=![]() m,
m,
∵S△PCQ=S△POC=![]() k,
k,
∴S△PEB=S△PCQ-S四边形CQBE=![]() k
k![]() m=
m=![]() ,故此选项正确; ④正确,
,故此选项正确; ④正确,
∵BE∥OQ,
∴△PEB∽∽△PCQ,
∴ 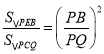 ,
,
∵S△PCQ=![]() k,S△PEB=
k,S△PEB=![]() ,
, 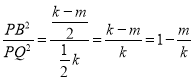 ,
,
∵ ![]() ,
,
∴ ![]() ,
,
∴OA2+PB2=PQ2,故此选项正确. 综上,选项正确的个数为4个 故选A.

 53随堂测系列答案
53随堂测系列答案【题目】某校学生会为了解本校学生每天体育锻炼所用时间情况,采用问卷的方式对一部分学生进行调查确定调查对象时,大家提出以下几种方案:(A)对各班体育委员进行调査;(B)对某班的全体学生进行调查;(C)从全校每班随机抽5名学生进行调查在问卷调查时,每位被调查的学都选择了问卷中适合自己的十个时间段,学生会将收集到的数据整理后续制成如下的统计表:
被调查的学生每天体育锻炼所用时间统计表
组别 | 时间x(小时) | 频数 |
一 | 0≤x≤0.5 | 15 |
二 | 0.6<x≤1 | 27 |
三 | 1<x≤1.5 | 38 |
四 | 1.5<x≤2 | 13 |
五 | x>2 | 7 |
(1)为了使收集到的数据具有代表性,学生会在确定调查对象时选择了方案 (填A、B或C);
(2)被调查的学生每天体育锻炼所用时间的中位数落在 组;
(3)根据以上统计结果,估计该校900名学生中每天体育锻炼时间不超过0.5小时的人数,并根据你计算的结果提出一条合理化建议.