题目内容
【题目】如图,在平面直角坐标系中,点P(﹣1,m)是双曲线y=![]() 上的一个点,过点P作PQ⊥x轴于点Q,连接PO,△OPQ的面积为3.
上的一个点,过点P作PQ⊥x轴于点Q,连接PO,△OPQ的面积为3.

(1)求m的值和双曲线对应的函数表达式;
(2)若经过点P的一次函数y=kx+b(k≠0、b≠0)的图象与x轴交于点A,与y交于点B且PB=2AB,求k的值.
【答案】(1)m=6,y=﹣![]() ; (2)k=﹣4或﹣12.
; (2)k=﹣4或﹣12.
【解析】
(1)根据反比例函数k的几何意义,求出n的值即可解决问题;
(2)分3种情形讨论,①当点A在x轴正半轴上时,由OB∥PQ,可得OB:PQ=AB:AP=1:3,继而求出OB=2,即B(0,2),待定系数法求一次函数解析式即可; ②当点A在x轴负半轴上时,由于PB=2AB,显然这种情形不存在;③当点B在y轴负半轴上时,
由于PB=2AB,可得PA=PB,根据PQ∥OB,可得![]() ,即QA=AO=
,即QA=AO=![]() ,
,
求出A(﹣![]() ,0),待定系数法求一次函数解析式即可.
,0),待定系数法求一次函数解析式即可.
(1)∵过点P作PQ⊥x轴于点Q,连接PO,△OPQ的面积为3,
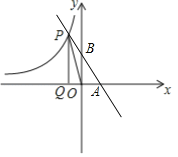
∴![]() ,
,
∵n<0,
∴n=﹣6,
∴反比例函数的解析式为y=﹣![]() ,
,
∴P(﹣1,6),
∴m=6,y=﹣![]() .
.
(2)①当点A在x轴正半轴上时,
∵OB∥PQ,
∴OB:PQ=AB:AP=1:3,
∴OB=2,
∴B(0,2),
把P(﹣1,6),B(0,2)代入y=kx+b中得到![]() ,
,
解得![]() .
.
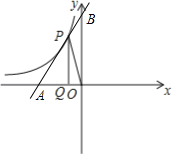
②当点A在x轴负半轴上时,∵PB=2AB,显然这种情形不存在.
③当点B在y轴负半轴上时,
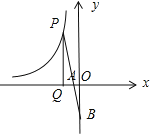
∵PB=2AB,
∴PA=PB,
∵PQ∥OB,
∴![]() ,
,
∴QA=AO=![]() ,
,
∴A(﹣![]() ,0),
,0),
把P(﹣1,6),A(﹣![]() ,0)代入y=kx+b中得到
,0)代入y=kx+b中得到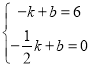 ,
,
解得![]() ,
,
综上所述,k=﹣4或﹣12.

 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案【题目】为了了解某校学生的课外阅读情况,随机抽查了10学生周阅读用时数,结果如下表:
周阅读用时数(小时) | 4 | 5 | 8 | 12 |
学生人数(人) | 2 | 1 | 3 | 4 |
则关于这10名学生周阅读所用时间,下列说法正确的是( )
A.中位数是6.5B.众数是12C.平均数是3.9D.方差是6
【题目】随着人们生活水平的提高,家用轿车越来越多地进入家庭.王先生家中买了一辆小轿车,他连续记录了7天中每天行驶的路程(如下表),以50km为标准,多于50km的记为“+”,不足50km的记为“﹣”,刚好50km的记为“0”.
第一天 | 第二天 | 第三天 | 第四天 | 第五天 | 第六天 | 第七天 | |
路程(km) | ﹣8 | ﹣11 | ﹣14 | 0 | ﹣16 | +41 | +15 |
(1)王先生这七天中平均每天驾车行驶多少千米?
(2)若每行驶1km需用汽油0.1升,汽油价格为6.5元/升,则王先生家一个月(按30天计)的汽油费用是多少元?
【题目】为了解某校学生对《最强大脑》、《朗读者》、《中国诗词大会》、《出彩中国人》四个电视节目的喜爱情况,随杋抽取了![]() 名学生进行调查统计(要求每名学生选出并且只能选出一个自己最喜爱的节目),并将调查结果绘制成如图统计图表:
名学生进行调查统计(要求每名学生选出并且只能选出一个自己最喜爱的节目),并将调查结果绘制成如图统计图表:
学生最喜爱的节目人数统计表
节目 | 人数(名) | 百分比 |
最强大脑 | 5 | 10% |
朗读者 | 15 | |
中国诗词大会 |
| 40% |
出彩中国人 | 10 | 20% |
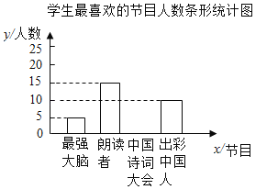
根据以上信息,回答下列问题:
(1)![]() ,
,![]() ;
;
(2)补全上面的条形统计图;
(3)若该校共有学生![]() 名,估计该校学生最喜爱《朗读者》节目的人数.
名,估计该校学生最喜爱《朗读者》节目的人数.