题目内容
(2012•河源)如图,矩形OABC中,A(6,0),C(0,2
),D(0,3
),射线l过点D且与x轴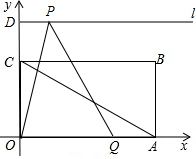 平行,点P、Q分别是l和x轴的正半轴上的动点,满足∠PQO=60°.
平行,点P、Q分别是l和x轴的正半轴上的动点,满足∠PQO=60°.
(1)①点B的坐标是
(2)设点P的横坐标为x,△OPQ与矩形OABC的重叠部分的面积为S,试求S与x的函数关系式和相应的自变量x的取值范围.
| 3 |
| 3 |
 平行,点P、Q分别是l和x轴的正半轴上的动点,满足∠PQO=60°.
平行,点P、Q分别是l和x轴的正半轴上的动点,满足∠PQO=60°.(1)①点B的坐标是
(6,2
)
| 3 |
(6,2
)
;②∠CAO=| 3 |
30
30
度;③当点Q与点A重合时,点P的坐标为(3,3
)
| 3 |
(3,3
)
;(直接填写答案)| 3 |
(2)设点P的横坐标为x,△OPQ与矩形OABC的重叠部分的面积为S,试求S与x的函数关系式和相应的自变量x的取值范围.
分析:(1)①由四边形OABC是矩形,根据矩形的性质,即可求得点B的坐标;②由正切函数,即可求得∠CAO的度数,③由三角函数的性质,即可求得点P的坐标;
(2)分别从当0≤x≤3时,当3<x≤5时,当5<x≤9时,当x>9时去分析求解即可求得答案.
(2)分别从当0≤x≤3时,当3<x≤5时,当5<x≤9时,当x>9时去分析求解即可求得答案.
解答: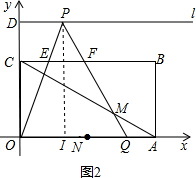
 解:(1)①∵四边形OABC是矩形,
解:(1)①∵四边形OABC是矩形,
∴AB=OC,OA=BC,
∵A(6,0)、C(0,2
),
∴点B的坐标为:(6,2
);
②∵tan∠CAO=
=
=
,
∴∠CAO=30°;
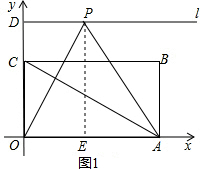
③如图1:当点Q与点A重合时,过点P作PE⊥OA于E,
∵∠PQO=60°,D(0,3
),
∴PE=3
,
∴AE=
=3,
∴OE=OA-AE=6-3=3,
∴点P的坐标为(3,3
);
故答案为:①(6,2
),②30,③(3,3
);
(2)当0≤x≤3时,
如图2,OI=x,IQ=PI•tan60°=3,OQ=OI+IQ=3+x;
由题意可知直线l∥BC∥OA,
可得
=
=
=
=
,
EF=
(3+x),
此时重叠部分是梯形,其面积为:
S梯形=
(EF+OQ)•OC=
(3+x);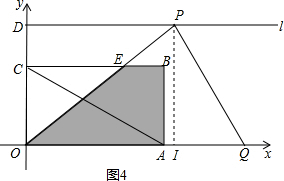
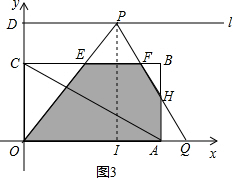
如图3,当3<x≤5时,∵AQ=OI+IQ-OA=x+3-6=x-3,
则AH=
(x-3),
则S=S梯形EFQO-S△HAQ=S梯形EFQO-
AH•AQ
=
(3+x)-
(x-3)2,
=-
x2+
x-
如图4,当5<x≤9时,∵CE∥DP,
∴
=
,
∴
=
,
∴CE=
x,
∴BE=6-
x,
 ∴S=
∴S=
(BE+OA)•OC=
(12-
x),
如图5,当9<x时,∵AH∥PI,
∴
=
,
∴
=
,
∴AH=
,
∵AO=6,
∴S=
OA•AH=
.

 解:(1)①∵四边形OABC是矩形,
解:(1)①∵四边形OABC是矩形,∴AB=OC,OA=BC,
∵A(6,0)、C(0,2
| 3 |
∴点B的坐标为:(6,2
| 3 |
②∵tan∠CAO=
| OC |
| OA |
2
| ||
| 6 |
| ||
| 3 |
∴∠CAO=30°;
③如图1:当点Q与点A重合时,过点P作PE⊥OA于E,
∵∠PQO=60°,D(0,3
| 3 |
∴PE=3
| 3 |
∴AE=
| PE |
| tan60° |
∴OE=OA-AE=6-3=3,
∴点P的坐标为(3,3
| 3 |
故答案为:①(6,2
| 3 |
| 3 |

(2)当0≤x≤3时,
如图2,OI=x,IQ=PI•tan60°=3,OQ=OI+IQ=3+x;
由题意可知直线l∥BC∥OA,
可得
| EF |
| OQ |
| PE |
| PO |
| DC |
| DO |
| ||
3
|
| 1 |
| 3 |
EF=
| 1 |
| 3 |
此时重叠部分是梯形,其面积为:
S梯形=
| 1 |
| 2 |
4
| ||
| 3 |

如图3,当3<x≤5时,∵AQ=OI+IQ-OA=x+3-6=x-3,
则AH=
| 3 |
则S=S梯形EFQO-S△HAQ=S梯形EFQO-
| 1 |
| 2 |
=
4
| ||
| 3 |
| ||
| 2 |
=-
| ||
| 2 |
13
| ||
| 3 |
| ||
| 2 |
如图4,当5<x≤9时,∵CE∥DP,
∴
| CO |
| DO |
| CE |
| DP |
∴
2
| ||
3
|
| CE |
| x |
∴CE=
| 2 |
| 3 |
∴BE=6-
| 2 |
| 3 |
 ∴S=
∴S=| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
如图5,当9<x时,∵AH∥PI,
∴
| AO |
| OI |
| AH |
| PI |
∴
| 6 |
| x |
| AH | ||
3
|
∴AH=
18
| ||
| x |
∵AO=6,
∴S=
| 1 |
| 2 |
54
| ||
| x |
点评:此题考查了矩形的性质,相似三角形的判定与性质、等腰三角形的性质以及直角三角形的性质等知识.此题综合性较强,难度较大,注意数形结合思想与分类讨论思想的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
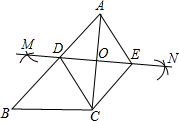 (2012•河源)如图,已知△ABC,按如下步骤作图:
(2012•河源)如图,已知△ABC,按如下步骤作图: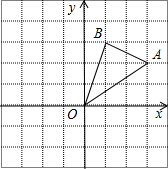 (2012•河源)如图,在边长为1的正方形组成的网格中,△AOB的顶点均在格点上,点A、B的坐标分别是A(3,2)、B(1,3).△AOB绕点O逆时针旋转90°后得到△A1OB1.(直接填写答案)
(2012•河源)如图,在边长为1的正方形组成的网格中,△AOB的顶点均在格点上,点A、B的坐标分别是A(3,2)、B(1,3).△AOB绕点O逆时针旋转90°后得到△A1OB1.(直接填写答案) (2012•河源)如图,连接在一起的两个正方形的边长都为1cm,一个微型机器人由点A开始按ABCDEFCGA…的顺序沿正方形的边循环移动.①第一次到达G点时移动了
(2012•河源)如图,连接在一起的两个正方形的边长都为1cm,一个微型机器人由点A开始按ABCDEFCGA…的顺序沿正方形的边循环移动.①第一次到达G点时移动了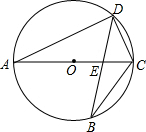 (2012•河源)如图,AC是⊙O的直径,弦BD交AC于点E.
(2012•河源)如图,AC是⊙O的直径,弦BD交AC于点E.