Question

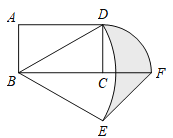
【题目】如图，已知矩形ABCD的两条边AB＝1，AD＝，以B为旋转中心，将对角线BD顺时针旋转60°得到线段BE，再以C为圆心将线段CD顺时针旋转90°得到线段CF，连接EF，则图中阴影部分面积为_____．

Answer 1

【答案】

【解析】

矩形ABCD的两条边AB＝1，AD＝，得到∠DBC＝30°，由旋转的性质得到BD＝BE，∠BDE＝60°，求得∠CBE＝∠DBC＝30°，连接CE，根据全等三角形的性质得到∠BCE＝∠BCD＝90°，推出D，C，E三点共线，得到CE＝CD＝1，根据三角形和扇形的面积公式即可得到结论．

∵矩形ABCD的两条边AB＝1，AD＝，

∴，

∴∠DBC＝30°，

∵将对角线BD顺时针旋转60°得到线段BE，

∴BD＝BE，∠BDE＝60°，

∴∠CBE＝∠DBC＝30°，

连接CE，

∴△DBC≌△EBC（SAS），

∴∠BCE＝∠BCD＝90°，

∴D，C，E三点共线，

∴CE＝CD＝1，

∴图中阴影部分面积＝S△BEF+S△BCD+S扇形DCF﹣S扇形DBE

＝+﹣

＝，

故答案为：．