��Ŀ����
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��y=![]() ��������y=��
��������y=��![]() x2+bx+c����A��B���㣬��A��x���ϣ���B�ĺ�����Ϊ��8��
x2+bx+c����A��B���㣬��A��x���ϣ���B�ĺ�����Ϊ��8��
��1����������ߵĽ���ʽ��
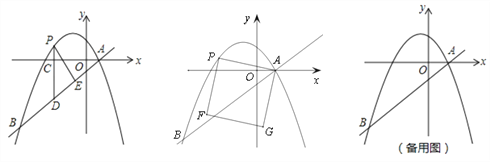
��2����P��ֱ��AB�Ϸ�����������һ���㣨�����A��B�غϣ�������P��x��Ĵ��ߣ�����ΪC����ֱ��AB�ڵ�D����PE��AB�ڵ�E��
�����PDE���ܳ�Ϊm����P�ĺ�����Ϊx������PDE�ܳ�m���ʱ�����P�����꣬�����m������ֵ��
������PA����PAΪ����ͼʾһ���������APFG����ʱ�뷽����������APFG�������ŵ�P���˶��������εĴ�С��λ��Ҳ��֮�ı䣮������F��Gǡ������y����ʱ��ֱ��д����Ӧ�ĵ�P�����꣮
���𰸡���1��![]() ��2���ٵ�x=��3ʱ�����ֵΪ15�ڴ��ڵ�P1��
��2���ٵ�x=��3ʱ�����ֵΪ15�ڴ��ڵ�P1��![]() ��2����P2��
��2����P2��![]() ��2����P3��
��2����P3��![]() ��
��![]() ��
��
�������������������1������ֱ�߽���ʽ�����A��B�����꣬�����ô���ϵ��������κ�������ʽ��𣻣�2��������ֱ�߽���ʽ�������߽���ʽ��ʾ��PD��������ͬ�ǵ������������DPE=��BAO������ֱ��kֵ�����BAO�����Һ�����ֵ��Ȼ���ʾ��PE��DE���ٸ��������ε��ܳ���ʽ��ʽ�������ɵý⣬�ٸ��ݶ��κ�������ֵ�����𣻢ڷ֣�i����G��y����ʱ������P��PH��x����H�����������ε����ʿɵ�AP=AG����PAG=90�����������PAH=��AGO��Ȼ���������ǽDZ���֤����APH����GAOȫ�ȣ�����ȫ�������ζ�Ӧ����ȿɵ�PH=AO=2��Ȼ�����ö��κ�������ʽ��⼴�ɣ���ii����F��y����ʱ������PM��x����M����PN��y����N�����������ε����ʿɵ�AP=FP����APF=90�����ٸ���ͬ�ǵ������������APM=��FPN��Ȼ���������DZ߽���֤����APM����FPNȫ�ȣ�����ȫ�������ζ�Ӧ����ȿɵ�PM=PN���Ӷ��õ���P�ĺ���������������ȣ��ٸ��ݶ��κ����Ľ���ʽ��⼴�ɣ�
���������
��1����y=0����![]() x��
x��![]() =0�����x=2��
=0�����x=2��
x=��8ʱ��y=![]() ������8����
������8����![]() =��
=��![]() ��
��
���A��2��0����B����8����![]() ����
����
�ѵ�A��B���������ߵã�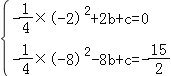 ��
��
���![]() ��
��
���ԣ��������ߵĽ���ʽ![]() ��
��
��2���١ߵ�P���������ϣ���D��ֱ���ϣ�
��PD=��![]() x2��
x2��![]() x+
x+![]() ����
����![]() x��
x��![]() ��=��
��=��![]() x2��
x2��![]() x+4��
x+4��
��PE��AB��
���DPE+��PDE=90�㣬
�֡�PD��x�ᣬ
���BAO+��PDE=90�㣬
���DPE=��BAO��
��ֱ�߽���ʽk=![]() ��
��
��sin��BAO=![]() ��cos��BAO=
��cos��BAO=![]() ��
��
��PE=PDcos��DPE=![]() PD��
PD��
DE=PDsin��DPE=![]() PD��
PD��
���PDE���ܳ�Ϊm=PD+![]() PD+
PD+![]() PD=
PD=![]() PD=
PD=![]() ����
����![]() x2��
x2��![]() x+4��=��
x+4��=��![]() x2��
x2��![]() x+
x+![]() ��
��
��m=��![]() x2��
x2��![]() x+
x+![]() ��
��
��m=��![]() ��x2+6x+9��+15��
��x2+6x+9��+15��
�൱x=��3ʱ�����ֵΪ15��
�ڡߵ�A��2��0����
��AO=2��
�֣�i����G��y����ʱ������P��PH��x����H��
��������APFG�У�AP=AG����PAG=90�㣬
�ߡ�PAH+��OAG=90�㣬��AGO+��OAG=90�㣬
���PAH=��AGO��
�ڡ�APH�͡�GAO�У�
 ��
��
���APH�ա�GAO��AAS����

��PH=AO=2��
���P��������Ϊ2��
�ੁ![]() x2��
x2��![]() x+
x+![]() =2��
=2��
�����ã�x2+3x��2=0��
���x=![]() ��
��
���P1��![]() ��2����P2��
��2����P2��![]() ��2����
��2����
��ii����F��y����ʱ������PM��x����M����PN��y����N��
��������APFG�У�AP=FP����APF=90�㣬
�ߡ�APM+��MPF=90�㣬��FPN+��MPF=90�㣬
���APM=��FPN��
�ڡ�APM�͡�FPN�У�
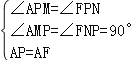 ��
��
���APM�ա�FPN��AAS����
��PM=PN��
���P�ĺ���������������ȣ�
�ੁ![]() x2��
x2��![]() x+
x+![]() =x��
=x��
�����ã�x2+7x��10=0��
���x1=![]() ��x2=
��x2=![]() ����ȥ����
����ȥ����
���P3��![]() ��
��![]() ��
��
�������������ڵ�P1��![]() ��2����P2��
��2����P2��![]() ��2����P3��
��2����P3��![]() ��
��![]() ����
����


