题目内容
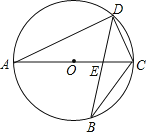
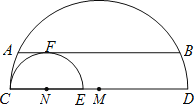
【题目】如图,直径分别为CD、CE的两个半圆相切于点C,大半圆M的弦与小半圆N相切于点F,且AB∥CD,AB=4,设![]() 、
、![]() 的长分别为x、y,线段ED的长为z,则z(x+y)的值为 .
的长分别为x、y,线段ED的长为z,则z(x+y)的值为 .
【答案】8π.
【解析】
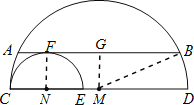
试题分析:过M作MG⊥AB于G,连MB,NF,根据垂径定理得到BG=AG=2,利用勾股定理可得MB2﹣MG2=22=4,再根据切线的性质有NF⊥AB,而AB∥CD,得到MG=NF,设⊙M,⊙N的半径分别为R,r,则z(x+y)=(CD﹣CE)(πR+πr)=(R2﹣r2)2π,即可得到z(x+y)的值.
解:过M作MG⊥AB于G,连MB,NF,如图,
而AB=4,
∴BG=AG=2,
∴MB2﹣MG2=22=4,
又∵大半圆M的弦与小半圆N相切于点F,
∴NF⊥AB,
∵AB∥CD,
∴MG=NF,
设⊙M,⊙N的半径分别为R,r,
∴z(x+y)=(CD﹣CE)(πR+πr),
=(2R﹣2r)(R+r)π,
=(R2﹣r2)2π,
=42π,
=8π.
故答案为:8π.

练习册系列答案
相关题目