题目内容
【题目】如图,∠ACB=∠ADB=90°,M、N 分别是 AB、CD 的中点.

(1)求证:MN⊥CD;
(2)若 AB=50,CD=48,求 MN 的长.
【答案】(1)证明见详解;
(2)7.
【解析】
(1)根据直角三角形的斜边上的中线等于斜边的一半得出![]() ,
,![]() ,再利用N是CD的中点,得出△DMN≌△CMN,求出MN垂直CD;
,再利用N是CD的中点,得出△DMN≌△CMN,求出MN垂直CD;
(2)利用AB=50,CD=48,求出CN=24,CM=25,由勾股定理求出NM即可.
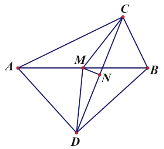
解:(1)∵∠ACB=∠ADB=90°,M、N分别是AB、CD的中点,
∴![]() ,
,![]() ,
,
∴MC=MD,
∵N是CD的中点,
在△DMN和△CMN中,
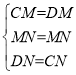
∴△DMN≌△CMN(SSS),
∴∠MNC=∠MND=90°,
∴MN⊥CD;
(2)∵AB=50,
∴DM=CM=25,
∵CD=48,MN垂直CD,N是CD的中点,
∴CN=24,
∴![]() .
.

练习册系列答案
相关题目