题目内容
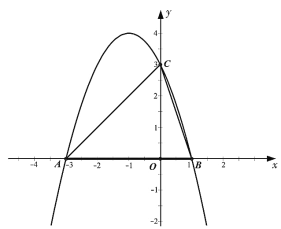
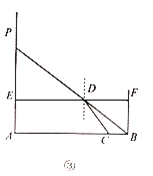
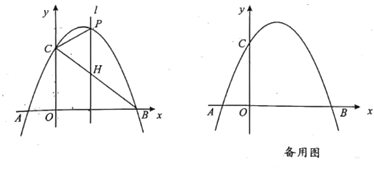
【题目】如图,已知抛物线y=ax2+bx+3与x轴交于点A(-1,0),B(3,0),与y轴交于点C。
(1)求抛物线的解析式;
(2)点P是第一象限抛物线上一动点,过点P作x轴的垂线![]() ,交BC于点H.当点P运动到何处时满足PC=CH?求出此时点P的坐标;
,交BC于点H.当点P运动到何处时满足PC=CH?求出此时点P的坐标;
(3)若m≤x≤m+1时,二次函数y=ax2+bx+3的最大值为m,求m的值.
【答案】(1)![]() ;(2)点P的坐标为(1,4);(3)m的值为
;(2)点P的坐标为(1,4);(3)m的值为![]() 或
或![]() .
.
【解析】
(1)将点A、B坐标代入抛物线解析式求出a,b值即可;
(2)求出直线BC的解析式,因点P在抛物线上,点H在直线上,故可设点P坐标为(x, ![]() ),则点H坐标为(x,-x+3),可得CM、PH的长,过点C作CM⊥PH于M,由等腰三角形的性质可得CM与PH间的数量关系,列出等式,求解即可;
),则点H坐标为(x,-x+3),可得CM、PH的长,过点C作CM⊥PH于M,由等腰三角形的性质可得CM与PH间的数量关系,列出等式,求解即可;
(3)分类讨论,若m+1≤1时函数在x=m+1处有最大值为m,若m<1<m+1,函数在x=1处有最大值,若m>1,函数在x=m处有最大值,再分别求解即可.
解:(1)由题意得![]()
解得![]()
∴抛物线的解析式为![]()
(2)设直线BC的解析式为y=kx+b
由题意得![]() ∴直线BC的解析式为y= -x+3.
∴直线BC的解析式为y= -x+3.
设点P坐标为(x, ![]() ),则点H坐标为(x,-x+3).
),则点H坐标为(x,-x+3).
由此可得,CM=x,PH=![]()
过点C作CM⊥PH于M
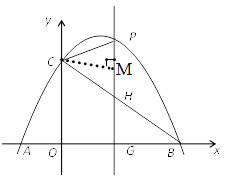
∵CP=CH ∴PM=MH, ∠MCH=∠MCP
∵OB=OC ∴∠OBC=45°
∵CM∥OB ∴∠MCH=∠OBC=45°∴∠PCH=90°
∴MC=![]() 即
即![]()
解得x1=0(舍) x2=1
∴当x=1时,y=4即点P的坐标为(1,4)
(3)若m+1≤1,即m≤0时,
当x=m+1时,函数有最大值为-(m+1)2+2(m+1)+3=m,
解得![]() (舍)
(舍) ![]() ;
;
若m<1<m+1,即0<m<1,
当
若m>1,
当x=m时,函数有最大值为-m2+2m+3=m,
解得 ![]()
![]() (舍);
(舍);
综上所述,m的值为![]() 或
或![]() .
.