题目内容
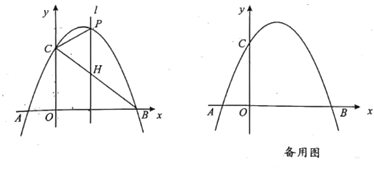
【题目】如图,抛物线与![]() 轴相交于点
轴相交于点![]() 、点
、点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 是抛物线上一动点, 联结
是抛物线上一动点, 联结![]() 交线段
交线段![]() 于点
于点![]() .
.
(1)求这条抛物线的解析式,并写出顶点坐标;
(2)求![]() 的正切值;
的正切值;
(3)当![]() 与
与![]() 相似时,求点
相似时,求点![]() 的坐标.
的坐标.
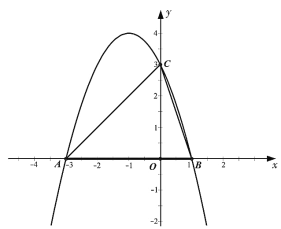
【答案】(1)![]() ,
,![]() ;(2)2;(3)点
;(2)2;(3)点![]() 的坐标为
的坐标为 或
或![]()
【解析】
(1)利用待定系数法确定函数解析式,根据函数解析式求得该抛物线的顶点坐标;
(2)如图,过点B作BH⊥AC于点H,构造等腰直角△ABH和直角△BCH,利用勾股定理和两点间的距离公式求得相关线段的长度,从而利用锐角三角函数的定义求得答案;
(3)如图2,过点D作DK⊥x轴于点K,构造直角△DOK,设D(x,x22x+3),则K(x,0).并由题意知点D位于第二象限.由于∠BAC是公共角,所以当△AOE与△ABC相似时,有2种情况:
①∠AOD=∠ABC.则tan∠AOD=tan∠ABC=3.由锐角三角函数定义列出比例式,从而求得点D的坐标.
②∠AOD=∠ACB.则tan∠AOD=tan∠ACB=2.由锐角三角函数定义列出比例式,从而求得点D的坐标.
(1)解:设抛物线的解析式为![]()
![]() 抛物线
抛物线![]() 过点
过点![]()

解得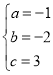
![]() 这条抛物线的解析式为
这条抛物线的解析式为![]()
顶点坐标为![]()
(2)解:过点![]() 作
作![]() ,垂足为
,垂足为![]()

![]()
![]()
![]()
![]()
![]()
![]() 在
在![]() 中,
中,![]()
![]()
![]()
![]()
![]()
(3)解:过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]()

设![]() ,则
,则![]() ,并由题意可得点
,并由题意可得点![]() 在第二象限
在第二象限
![]()
![]() 是公共角
是公共角
![]() 当
当![]() 与
与![]() 相似时
相似时
存在以下两种可能
①![]()
![]()
![]()
解得![]() ,
,![]() (舍去)
(舍去)

②![]()
![]()
![]()
解得![]() ,
,![]() (舍去)
(舍去)
![]()
综上所述:当![]() 与
与![]() 相似时,
相似时,
点![]() 的坐标为
的坐标为 或
或![]()

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目