Question

【题目】已知抛物线与轴交于、两点，将这条抛物线的顶点记为，连接、，则的值为（ ）

A.B.C.D.2

Answer 1

【答案】D

【解析】

设点A在点B的左侧，过点C作CD⊥AB于点D，将y=0代入y=x2-2x-3中即可求出点A、B的坐标，再利用配方法将抛物线的解析式由一般式变形为顶点式，由此即可得出点C的坐标，结合正切的定义即可得出tan∠CAB的值．

设点A在点B的左侧，过点C作CD⊥AB于点D，如图所示．

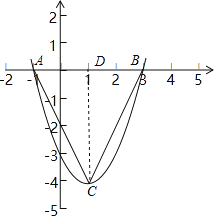
令y=x2-2x-3=（x+1）（x-3）=0，

解得：x1=-1，x2=3，

∴点A（-1，0），点B（3，0），

∵y=x2-2x-3=（x-1）2-4，

∴点C（1，-4），

∴点D（1，0），

∵AD=1-（-1）=2，CD=0-（-4）=4，

∴tan∠CAB===2．

故选：D．