Question

【题目】如图，已知抛物线y=ax2+bx+c（a≠0）与x轴交于点A（﹣4，0），B（1，0），与y轴交于点D（0，4），点C（﹣2，n）也在此抛物线上．

（1）求此抛物线的解析式及点C的坐标；

（2）设BC交y轴于点E，连接AE，AC请判断△ACE的形状，并说明理由；

（3）连接AD交BC于点F，试问：以A，B，F为顶点的三角形与△ABC相似吗？请说明理由．

Answer 1

【答案】(1)、y=﹣x2﹣3x+4；C(-2，6)；(2)、等腰直角三角形；理由见解析；(3)、相似；理由见解析.

【解析】

试题分析：(1)、由A、B、D三点坐标，利用待定系数法可求得抛物线解析式，把C点坐标代入解析式可求得n的值，可求得C点坐标；(2)、把C点坐标代入抛物线解析式可求得n，可得C点坐标，利用待定系数法可求得直线BC的解析式，则可求得E点坐标，利用勾股定理可求得AC、AE、CE的长，则可判断△ACE的形状；(3)、由A、D坐标可先求得直线AD解析式，联立直线BC、AD解析式可求得F点坐标，又可求得BF、BC和AB的长，由题意可知∠ABF=∠CAB，若以A，B，F为顶点的三角形与△ABC相似只有∠BFA=∠CAB，则判定和是否相等即可．

试题解析：(1)、∵抛物线经过A、B、D三点，

∴代入抛物线解析式可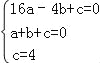得，解得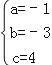， ∴抛物线y=﹣x2﹣3x+4，

∵点C（﹣2，n）也在此抛物线上， ∴n=﹣4+6+4=6， ∴C点坐标为（﹣2，6）；

(2)、△ACE为等腰直角三角形，理由如下： 设直线BC解析式为y=kx+s，

把B、C两点坐标代入可得，解得， ∴直线BC解析式为y=﹣2x+2，

令x=0可得y=2， ∴E点坐标为（0，2）， ∵A（﹣4，0），C（﹣2，6），

∴AC===2，AE===2，CE===2，

∴AE2+CE2=20+20=40=AC2，且AE=CE， ∴△ACE为等腰直角三角形；

(3)、相似，理由如下： 设直线AD解析式为y=px+q，

把A、D坐标代入可得，解得， ∴直线AD解析式为y=x+4，

联立直线AD、BC解析式可得，解得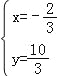， ∴F点坐标为（﹣，），

∴BF==，BC==3，且AB=1﹣（﹣4）=5，

∴==， ==， ∴=，且∠BFA=∠CAB， ∴△ABF∽△CBA．