题目内容
如图，以O为圆心的两个同心圆中，大圆的弦AB是小圆的切线，C为切点．若两圆的半径分别为Rcm和rcm，AB的长为8cm，则圆环的面积为16π
16π
平方厘米．分析：连接OA、OB，根据勾股定理可得OB2-OC2=BC2，而圆环的面积等于=π•OB2-π•OC2=π（OB2-OC2），据此即可求解．
解答：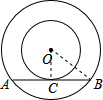
解：连接OA、OB．
∵AB是小圆的切线，
∴OC⊥AB．
∴OB2-OC2=BC2=16，
∴S圆环=π•OB2-π•OC2=π（OB2-OC2）=16π（cm2）．
故答案是：16π．
解：连接OA、OB．∵AB是小圆的切线，
∴OC⊥AB．
∴OB2-OC2=BC2=16，
∴S圆环=π•OB2-π•OC2=π（OB2-OC2）=16π（cm2）．
故答案是：16π．
点评：本题考查了切线的性质定理和勾股定理，正确理解切线的性质定理是关键．
练习册系列答案
相关题目
圆于点C，过点C作直线CE⊥AD，垂足为E，交大圆于F，H两点．
如图，以O为圆心的两个同心圆中，大圆的弦AB切小圆于P，如果AB=4cm，则图中阴影部分的面积为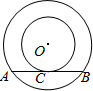
如图，以O为圆心的两个同心圆中，大圆的弦AB是小圆的切线，C为切点，若两圆的半径分别为3cm和5cm，则AB的长为
如图，以O为圆心的两个同心圆中，大圆的弦AB是小圆的切线，切点为C，若AB=