题目内容
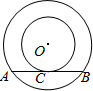如图，以O为圆心的两个同心圆中，大圆的弦AB是小圆的切线，C为切点．若两圆的半径分别为6cm和10cm，则AB的长为16
16
cm．分析：连接OC，OB，由大圆的弦AB为小圆的切线，可得出OC垂直于AB，由垂径定理得到C为AB的中点，在直角三角形OBC中，由OB及OC的长，利用勾股定理求出BC的长，再根据AB=2BC可得出AB的长．
解答：解：连接OC，OB，
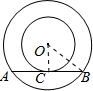
∵AB为圆O的切线，∴OC⊥AB，
∴C为AB的中点，即AC=BC=
AB，
又∵OB=10cm，OC=6cm，
在Rt△OBC中，根据勾股定理得：BC=
=8cm，
则AB=2BC=16cm．
故答案为：16
∵AB为圆O的切线，∴OC⊥AB，
∴C为AB的中点，即AC=BC=
| 1 |
| 2 |
又∵OB=10cm，OC=6cm，
在Rt△OBC中，根据勾股定理得：BC=
| OB2-OC2 |
则AB=2BC=16cm．
故答案为：16
点评：此题考查了切线的性质，垂径定理，以及勾股定理，熟练掌握性质及定理是解本题的关键．
练习册系列答案
相关题目
圆于点C，过点C作直线CE⊥AD，垂足为E，交大圆于F，H两点．
如图，以O为圆心的两个同心圆中，大圆的弦AB切小圆于P，如果AB=4cm，则图中阴影部分的面积为
如图，以O为圆心的两个同心圆中，大圆的弦AB是小圆的切线，切点为C，若AB=