题目内容
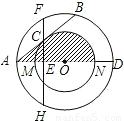
(附加题)如图,以O为圆心的两个同心圆中,大圆的直径AD交小圆于M,N两点,大圆的弦AB切小 圆于点C,过点C作直线CE⊥AD,垂足为E,交大圆于F,H两点.
圆于点C,过点C作直线CE⊥AD,垂足为E,交大圆于F,H两点.(1)试判断线段AC与BC的大小关系,并说明理由;
(2)求证:FC•CH=AE•AO;
(3)若FC,CH是方程x2-2
| 5 |
分析:(1)相等,主要根据是垂径定理,从已知条件中可知AB为大圆的弦,且垂直于半径,所以相等.
(2)利用切线定理,和相交弦定理就可证明.
(3)先解方程求出根,再观察图发现阴影部分图形的周长就是一段弧长加一线段,分别计算相加.
(2)利用切线定理,和相交弦定理就可证明.
(3)先解方程求出根,再观察图发现阴影部分图形的周长就是一段弧长加一线段,分别计算相加.
解答:(1)解:相等.(1分)
连接OC,则CO⊥AB,故AC=BC.
(2)证明:连接FB,AH,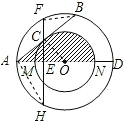 C0,
C0,
∵∠FBA=∠AHF,∠FCB=∠HCA,
∴△ACH∽△FCB,
∴AC•CB=FC•CH=AC2,
∵∠ACO=∠CEA=90°,∠CAO=∠CAO,
∴△ACE∽△AOC,得AC2=AE•AO.
∴FC•CH=AE•AO.
(3)解:解方程得:CH=
+1,CF=
-1,
CE=EF-FC=EH-FC=
-(
-1)=1,AC2=4,AC=2,
在Rt△ACE中,sinA=
=
,
∴∠A=30°,∴∠AOC=60°,∠CON=120°.
在△ACO中,CO=AC•tanA=2×
=
,
AO=
=
,AM=AO-OM=
-
=
,
长=
×2π•
=
π,
AN=AM+2OC=
+2×
=2
,
阴影部分周长=AC+AN+
=2+2
+
π.
连接OC,则CO⊥AB,故AC=BC.
(2)证明:连接FB,AH,
 C0,
C0,∵∠FBA=∠AHF,∠FCB=∠HCA,
∴△ACH∽△FCB,
∴AC•CB=FC•CH=AC2,
∵∠ACO=∠CEA=90°,∠CAO=∠CAO,
∴△ACE∽△AOC,得AC2=AE•AO.
∴FC•CH=AE•AO.
(3)解:解方程得:CH=
| 5 |
| 5 |
CE=EF-FC=EH-FC=
| 5 |
| 5 |
在Rt△ACE中,sinA=
| CE |
| AC |
| 1 |
| 2 |
∴∠A=30°,∴∠AOC=60°,∠CON=120°.
在△ACO中,CO=AC•tanA=2×
| ||
| 3 |
| 2 |
| 3 |
| 3 |
AO=
| AC |
| sin60° |
4
| ||
| 3 |
4
| ||
| 3 |
2
| ||
| 3 |
2
| ||
| 3 |
 |
| CN |
| 1 |
| 3 |
2
| ||
| 3 |
4
| ||
| 9 |
AN=AM+2OC=
2
| ||
| 3 |
2
| ||
| 3 |
| 3 |
阴影部分周长=AC+AN+
 |
| CN |
| 3 |
4
| ||
| 9 |
点评:[点评]本题是比较传统的几何型综合压轴题,涉及圆、相似、三角等几何重点知识.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
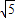 x+4=0的两根(CH>CF),求图中阴影部分图形的周长.
x+4=0的两根(CH>CF),求图中阴影部分图形的周长.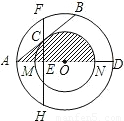
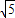 x+4=0的两根(CH>CF),求图中阴影部分图形的周长.
x+4=0的两根(CH>CF),求图中阴影部分图形的周长.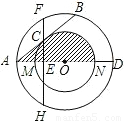
 x+4=0的两根(CH>CF),求图中阴影部分图形的周长.
x+4=0的两根(CH>CF),求图中阴影部分图形的周长.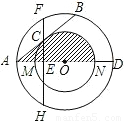
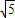 x+4=0的两根(CH>CF),求图中阴影部分图形的周长.
x+4=0的两根(CH>CF),求图中阴影部分图形的周长.