题目内容
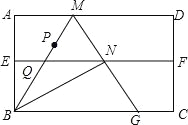
【题目】如图，将矩形纸片
沿对角线
折叠，点
落在点
处，
交
于点
，连结
．证明：（1）BF=DF．（2）若BC=8，DC=6，求BF的长。
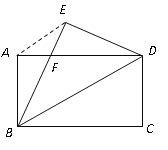
【答案】（1）证明见解析；(2)BF=6.25；
【解析】（1）由折叠的性质知，CD=ED，BE=BC．∵四边形ABCD是矩形，∴AD=BC，AB=CD，∠BAD=90°，∴AB=DE，BE=AD，在△ABD与△EDB中，∵AB=DE，BE=AD，BD=BD，∴△ABD≌△EDB（SSS），∴∠EBD=∠ADB，∴BF=DF；
（2）在△ABD与△EDB中，∵∠AFB=∠EFD，∠A=∠E=90°，AB=DE，∴△ABF≌△EDF（AAS），∴AF=EF，设BF=x，则AF=FE=8﹣x，在Rt△AFB中，可得：BF2=AB2+AF2，即x2=62+（8﹣x）2，解得：x=6.25．故BF的长为6.25．
练习册系列答案
相关题目
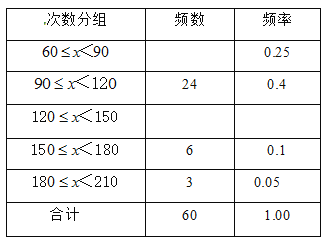
【题目】某校初二年级数学考试，（满分为100分，该班学生成绩均不低于50分）作了统计分析，绘制成如图频数分布直方图和频数、频率分布表，请你根据图表提供的信息，解答下列问题：
分组 | 49.5～59.5 | 59.5～69.5 | 69.5～79.5 | 79.5～89.5 | 89.5～100.5 | 合计 |
频数 | 2 | a | 20 | 16 | 4 | 50 |
频率 | 0.04 | 0.16 | 0.40 | 0.32 | b | 1 |
（1）频数、频率分布表中a= ，b= ；（答案直接填在题中横线上）
（2）补全频数分布直方图；
（3）若该校八年级共有600名学生，且各个班级学生成绩分布基本相同，请估计该校八年级上学期期末考试成绩低于70分的学生人数．
