题目内容
如图,已知抛物线C1:![]() 的顶点为P,与x轴相交于A、B两点(点A在点B的左边),点B的横坐标是1.
的顶点为P,与x轴相交于A、B两点(点A在点B的左边),点B的横坐标是1.
1.求P点坐标及a的值;
2.如图(1),

抛物线C2与抛物线C1关于x轴对称,将抛物线C2向右平移,平移后的抛物线记为C3,C3的顶点为M,当点P、M关于点B成中心对称时,求C3的解析式;
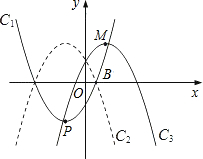
3.如图(2),

点Q是x轴正半轴上一点,将抛物线C1绕点Q旋转180°后得到抛物线C4.抛物线C4的顶点为N,与x轴相交于E、F两点(点E在点F的左边),当以点P、N、F为顶点的三角形是直角三角形时,求点Q的坐标.
1.由抛物线C1:![]() 得
得
顶点P的为(-2,-5) ………2分
∵点B(1,0)在抛物线C1上
∴![]()
解得,a= ………4分
2.连接PM,作PH⊥x轴于H,作MG⊥x轴于G

∵点P、M关于点B成中心对称
∴PM过点B,且PB=MB
∴△PBH≌△MBG
∴MG=PH=5,BG=BH=3
∴顶点M的坐标为(4,5) ………6分
抛物线C2由C1关于x轴对称得到,抛物线C3由C2平移得到
∴抛物线C3的表达式为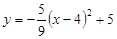 ………8分
………8分
3.∵抛物线C4由C1绕点x轴上的点Q旋转180°得到
∴顶点N、P关于点Q成中心对称
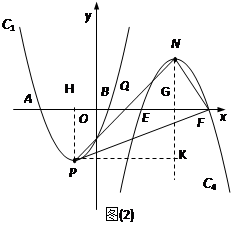
由(2)得点N的纵坐标为5
设点N坐标为(m,5) ………9分
作PH⊥x轴于H,作NG⊥x轴于G
作PK⊥NG于K
∵旋转中心Q在x轴上
∴EF=AB=2BH=6
∴FG=3,点F坐标为(m+3,0)
H坐标为(2,0),K坐标为(m,-5),
根据勾股定理得
PN2=NK2+PK2=m2+4m+104
PF2=PH2+HF2=m2+10m+50
NF2=52+32=34 ………10分
①当∠PNF=90º时,PN2+ NF2=PF2,解得m=,∴Q点坐标为(,0)
②当∠PFN=90º时,PF2+ NF2=PN2,解得m=,∴Q点坐标为(,0)
③∵PN>NK=10>NF,∴∠NPF≠90º
综上所得,当Q点坐标为(,0)或(,0)时,以点P、N、F为顶点
的三角形是直角三角形. ………12分
解析:略

 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案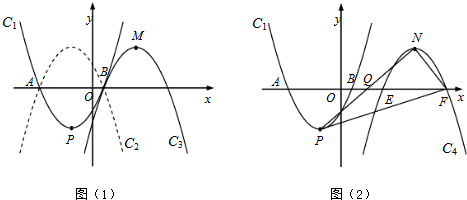


 的左侧),点B的横坐标是1;
的左侧),点B的横坐标是1;