题目内容
【题目】如图,![]() 中,
中,![]() ,
,![]() ,点
,点![]() 在直线
在直线![]() 上,
上,![]() 是等腰直角三角形,
是等腰直角三角形,![]() ,
,![]() ,连接
,连接![]() .
.
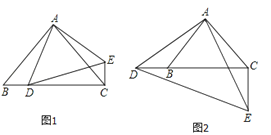
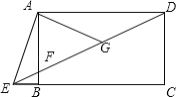
(1)当点![]() 在线段
在线段![]() 上时,如图1,求证:
上时,如图1,求证:![]() ;
;
(2)当点![]() 在线段
在线段![]() 延长线上时,如图2,求证:
延长线上时,如图2,求证:![]()
【答案】(1)见解析;(2)见解析.
【解析】
(1)利用△ABC是等腰直角三角形,易得AB=AC,∠BAC=90°,即有∠BAD+∠DAC=90°,同理可得AD=AE,∠DAC+∠CAE=90°,从而可证∠BAD=∠CAE,从而利用SAS可证△BAD≌△CAE,那么BD=CE,于是BC=CE+DC,再利用勾股定理可知BC=
![]() AC,进而可证DC+CE=
AC,进而可证DC+CE=![]() AC;
AC;
(2)同(1)可证△BAD≌△CAE,那么BD=CE,而BC+BD=CD,易证![]() AC=CDCE.
AC=CDCE.
解:(1)∵△ABC是等腰直角三角形,
∴AB=AC,∠BAC=90°,即∠BAD+∠DAC=90°,
同理有AD=AE,∠DAC+∠CAE=90°,
∴∠BAD=∠CAE,
∴△BAD≌△CAE(SAS),
∴BD=CE,
∴BC=CE+DC,
在Rt△ABC中,BC=![]() AC,
AC,
∴DC+CE=![]() AC;
AC;
(2)∵△ABC是等腰直角三角形,
∴AB=AC,∠BAC=90°,即∠BAE+∠EAC=90°,
同理有AD=AE,∠DAB+∠BAE=90°,
∴∠BAD=∠CAE,
∴△BAD≌△CAE(SAS),
∴BD=CE,
又∵BC+BD=CD,
∴BC=CDCE,即![]() AC=CDCE;
AC=CDCE;

 名校课堂系列答案
名校课堂系列答案【题目】滴滴快车是一种便捷的出行工具,计价规则如下表:
计费项目 | 里程费 | 时长费 | 远途费 |
单价 | 1.8元/公里 | 0.45元/分钟 | 0.4元/公里 |
注:车费由里程费、时长费、远途费三部分构成,其中里程费按行车的实际里程计算;时长费按行车的实际时间计算;远途费的收取方式为:行车里程10公里以内(含10公里)不收远途费,超过10公里的,超出部分每公里收0.4元. | |||
(1)若小东乘坐滴滴快车,行车里程为20公里,行车时间为30分钟,则需付车费________元.
(2)若小明乘坐滴滴快车,行车里程为a公里,行车时间为b分钟,则小明应付车费多少元(用含a、b的代数式表示,并化简.)
(3)小王与小张各自乘坐滴滴快车,行车里程分别为9.5公里与14.5公里,如果下车时两人所付车费相同,那么这两辆滴滴快车的行车时间相差多少分钟?