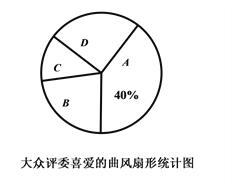
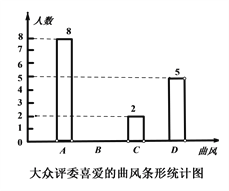
题目内容
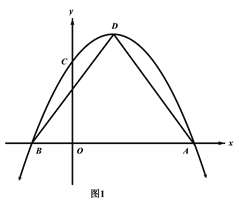
【题目】如图1,抛物线![]() 与x轴相交于A,B两点(点A在点B的右侧),与y轴交于点C,点D是抛物线的顶点,连接AD、BD.
与x轴相交于A,B两点(点A在点B的右侧),与y轴交于点C,点D是抛物线的顶点,连接AD、BD.
![]() 求△ABD的面积;
求△ABD的面积;
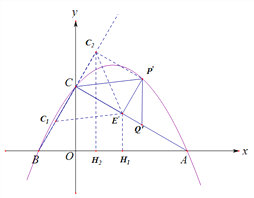
![]() 如图2,连接AC、BC,若点P是直线AC上方抛物线上一动点,过P作PE//BC交AC于点E,作PQ//y轴交AC于点Q,当△PQE周长最大时,将△PQE沿着直线AC平移,记移动中的△PQE为
如图2,连接AC、BC,若点P是直线AC上方抛物线上一动点,过P作PE//BC交AC于点E,作PQ//y轴交AC于点Q,当△PQE周长最大时,将△PQE沿着直线AC平移,记移动中的△PQE为![]() ,连接
,连接![]() ,求△PQE的周长的最大值及
,求△PQE的周长的最大值及![]() 的最小值;
的最小值;
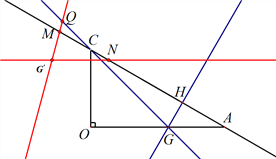
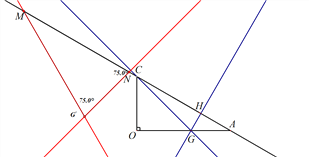
![]() 如图3,点G为x轴正半轴上一点,且OG=OC,连接CG,过G作GH⊥AC于点H,将△CGH绕点O顺时针旋转
如图3,点G为x轴正半轴上一点,且OG=OC,连接CG,过G作GH⊥AC于点H,将△CGH绕点O顺时针旋转![]() (
(![]() ),记旋转中的△CGH为
),记旋转中的△CGH为![]() ,在旋转过程中,直线
,在旋转过程中,直线![]() ,
,![]() 分别与直线AC交于点M,N,
分别与直线AC交于点M,N, ![]() 能否成为等腰三角形?若能直接写出所有满足条件的
能否成为等腰三角形?若能直接写出所有满足条件的![]() 的值;若不能,请说明理由.
的值;若不能,请说明理由.


【答案】(1)A(6,0),B(-2,0),![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ,
, ![]() ,
, ![]() .
.
【解析】分析: ![]() 令
令![]() 即可求出点
即可求出点![]() 的坐标,求出顶点坐标,即可计算面积.
的坐标,求出顶点坐标,即可计算面积.
![]() 用待定系数法求出直线
用待定系数法求出直线![]() 的解析式,设点
的解析式,设点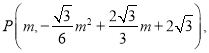 则
则
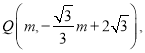 表示出
表示出![]() ,
, ![]() ,此时
,此时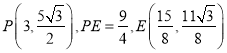 ,即可求出周长的最大值.
,即可求出周长的最大值.
如图, ![]() 平移后为
平移后为![]() ,再关于AC对称后为
,再关于AC对称后为![]() ,则
,则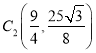 ,
,
求![]() 得最小值即可.
得最小值即可.
![]() 分三种请进行讨论.
分三种请进行讨论.
详解:(1)令![]() 解得:
解得: ![]()
![]()
![]()
即点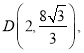
![]() .
.
(2)![]() ,
, ![]() ,
, ![]() ,
, 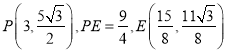
△PQE周长最大值为![]() ,
,
如图, ![]() 平移后为
平移后为![]() ,再关于AC对称后为
,再关于AC对称后为![]() ,则
,则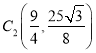 ,
,
![]()
![]()
(3)![]() ,
, ![]() ,
, ![]()
如图1,此时![]() ,
,![]() ,旋转角为
,旋转角为![]()

图1
如图2,此时旋转角为![]() 的补角,
的补角, ![]() ,
,![]() ,故旋转角为120°
,故旋转角为120°
如图3,旋转角![]() 180-(30-15)=165°
180-(30-15)=165°

练习册系列答案
相关题目