题目内容
已知二次函数y=x2-2（m-1）x+m2-2m-3的图象与函数y=-x2+6x的图象交于y轴一点，则m=________．
-1或3
分析：两函数图象交于y轴上一点，即横坐标为0，纵坐标相等，据此列方程即可解答．
解答：依题意，在y=-x2+6x中，x=0时，y=0；
在y=x2-2（m-1）x+m2-2m-3中，
x=0时，y=m2-2m-3=0；
即m2-2m-3=0，解得m=-1或3．
点评：本题涉及二次函数的综合性质，难度中等．
分析：两函数图象交于y轴上一点，即横坐标为0，纵坐标相等，据此列方程即可解答．
解答：依题意，在y=-x2+6x中，x=0时，y=0；
在y=x2-2（m-1）x+m2-2m-3中，
x=0时，y=m2-2m-3=0；
即m2-2m-3=0，解得m=-1或3．
点评：本题涉及二次函数的综合性质，难度中等．
练习册系列答案
名校课堂系列答案
相关题目
已知二次函数y=x2+（2a+1）x+a2-1的最小值为0，则a的值是（ ）
A、
| ||
B、-
| ||
C、
| ||
D、-
|
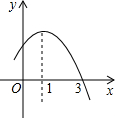已知二次函数y=-x2+2x+m的部分图象如图所示，则关于x的一元二次方程-x2+2x+m=0的解为（ ）| A、x1=1，x2=3 | B、x1=0，x2=3 | C、x1=-1，x2=1 | D、x1=-1，x2=3 |
已知二次函数y=-x2+bx+c的图象如图所示，它与x轴的一个交点坐标为（-1，0），与y轴的交点坐标为（0，3）．