题目内容
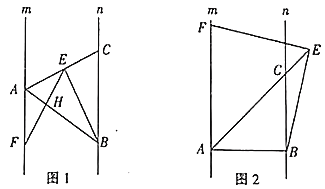
【题目】如图,在△ABC中,AB=AC,点D在边BC上,连接AD .
(1)试利用尺规作图,求作:线段AE,使得AE是线段AD绕点A沿逆时针方向旋转得到的,且![]() (保留作图痕迹,不写作法于证明过程);
(保留作图痕迹,不写作法于证明过程);
(2)连接DE交AC于F,若![]() ,求
,求![]() 的度数.
的度数.

【答案】(1)答案见解析;(2)65°
【解析】
(1)做∠MAC=∠DAB,然后以A为圆心,AD为半径画弧,交AM于点E,线段AE即为所求;
(2)连接CE,由题意证明△ABD≌△ACE,然后利用等腰三角形和全等三角形的性质,分别表示出∠BAC,∠ACE与∠B的关系,从而列方程求解.
解:(1)如图所示,即为所求
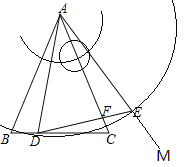
(2)连接CE
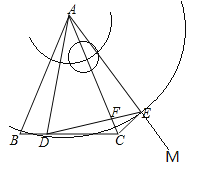
又题意可知“AB=AC,![]() ,AD=AE”
,AD=AE”
∴△ABD≌△ACE
∴∠B=∠ACE
∵![]()
∴∠BAC+∠CAE+∠AEC=165°
∵AB=AC
∴设∠B=x°,则∠BAC=(180-2x)°,∠ACE=x°
∴180-2x+180-x=165
解得:x=65
∴∠B的度数是65°

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目