题目内容
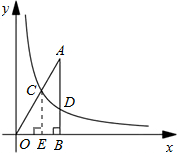
如图,已知点A的坐标为(
,3),AB⊥x轴,垂足为B,连接OA,反比例函数y=
(k>0)的图象与线段OA、AB分别交于点C、D.若AB=3BD,以点C为圆心,CA的长为半径作圆,则该圆与x轴的位置关系是______(填“相离”、“相切”或“相交”).

| 3 |
| k |
| x |

∵已知点A的坐标为(
,3),AB=3BD,
∴OA=2
,AB=3,BD=1,
∴D点的坐标为(
,1),
∴反比例函数y=
解析式为:y=
,
设AO直线解析式为:y=k′x,
3=
k′,
∴k′=
,
∴y=
x.
则
,
解得,
,或
(不合题意,舍去)
∴C(1,
),则OE=1,CE=
,
∴根据勾股定理知CO=2,
∴AC=2
-2.
∵AC-CE=2
-2-
=
-2<0,
∴AC<CE,
∴该圆与x轴的位置关系是相离.
故答案为:相离.
| 3 |
∴OA=2
| 3 |
∴D点的坐标为(
| 3 |
∴反比例函数y=
| k |
| x |
| ||
| x |
设AO直线解析式为:y=k′x,
3=
| 3 |
∴k′=
| 3 |
∴y=
| 3 |
则
|
解得,
|
|
∴C(1,
| 3 |
| 3 |
∴根据勾股定理知CO=2,
∴AC=2
| 3 |
∵AC-CE=2
| 3 |
| 3 |
| 3 |
∴AC<CE,
∴该圆与x轴的位置关系是相离.
故答案为:相离.


练习册系列答案
相关题目


 轴相交于C,D两点.
轴相交于C,D两点.