题目内容
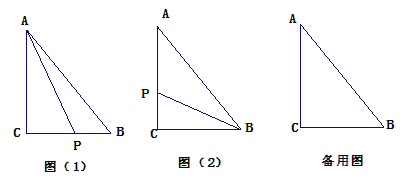
【题目】如图,Rt△OAB的顶点A(﹣2,4)在抛物线y=ax2上,将Rt△OAB绕点O顺时针旋转90°,得到△OCD,边CD与该抛物线交于点P,则点P的坐标为( )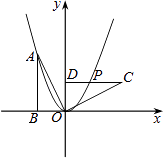
A.( ![]() ,
, ![]() )
)
B.(2,2)
C.( ![]() ,2)
,2)
D.(2, ![]() )
)
【答案】C
【解析】解:∵Rt△OAB的顶点A(﹣2,4)在抛物线y=ax2上,
∴4=a×(﹣2)2 ,
解得:a=1
∴解析式为y=x2 ,
∵Rt△OAB的顶点A(﹣2,4),
∴OB=OD=2,
∵Rt△OAB绕点O顺时针旋转90°,得到△OCD,
∴CD∥x轴,
∴点D和点P的纵坐标均为2,
∴令y=2,得2=x2 ,
解得:x=± ![]() ,
,
∵点P在第一象限,
∴点P的坐标为:( ![]() ,2)
,2)
故选:C.
首先根据点A在抛物线y=ax2上求得抛物线的解析式和线段OB的长,从而求得点D的坐标,根据点P的纵坐标和点D的纵坐标相等得到点P的坐标即可;

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目