题目内容
【题目】如图,直线y=﹣x+3与x轴、y轴分别交于点B、点C,经过B、C两点的抛物线y=x2+bx+c与x轴的另一个交点为A,顶点为P.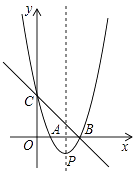
(1)求该抛物线的解析式;
(2)连接AC,在x轴上是否存在点Q,使以P、B、Q为顶点的三角形与△ABC相似?若存在,请求出点Q的坐标;若不存在,请说明理由.
【答案】
(1)
解:∵直线y=﹣x+3与x轴、y轴分别交于点B、点C,
令x=0,得y=3,
∴C(0,3),
令y=0,得x=3,
∴B(3,0),
∵经过B、C两点的抛物线y=x2+bx+c
∴ ![]() ,
,
解得 ![]() ,
,
∴抛物线解析式为y=x2﹣4x+3;
(2)
解:由(1),得A(1,0),连接BP,
∵∠CBA=∠ABP=45°,
∵抛物线解析式为y=x2﹣4x+3;
∴P(2,﹣1),
∵A(1,0),B(3,0),C(0,3),
∴BA=2,BC=3 ![]() ,BP=
,BP= ![]() ,
,
当△ABC∽△PBQ时,
∴ ![]() ,
,
∴ ![]() ,
,
∴BQ=3,
∴Q(0,0),
当△ABC∽△QBP时,
∴ ![]() ,
,
∴ ![]() ,
,
∴BQ= ![]() ,
,
∴Q( ![]() ,0),
,0),
∴Q点的坐标为(0,0)或( ![]() ,0).
,0).
【解析】(1)先确定出点B,C坐标,再用待定系数法求函数解析式;(2)先求出BA=2,BC=3 ![]() ,BP=
,BP= ![]() ,然后分两种情况①由△ABC∽△PBQ,得到
,然后分两种情况①由△ABC∽△PBQ,得到 ![]() ,求出BQ,②由△ABC∽△QBP得
,求出BQ,②由△ABC∽△QBP得 ![]() ,求出BQ,即可.
,求出BQ,即可.
【考点精析】本题主要考查了二次函数的图象的相关知识点,需要掌握二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点才能正确解答此题.

练习册系列答案
相关题目