题目内容
已知:⊙O的直径为3,线段AC=4,直线AC和PM分别与⊙O相切于点A,M.

(1)求证:点P是线段AC的中点;
(2)求sin∠PMC的值.

(1)求证:点P是线段AC的中点;
(2)求sin∠PMC的值.
解:(1)证明:如图,连接OM,

∵直线AC和PM分别与⊙O相切于点A,M,
∴PM=PA,OM⊥BC,BA⊥AC。
∴∠OMP=90°,∠BAC=90°。
∴∠1+∠2=90°,∠B+∠C=90°。
∵OB=OM,∴∠2=∠B。∴∠1=∠C。∴PC=PM。
又∵直线AC和PM分别与⊙O相切于点A,M,
∴PA=PM。∴PA=PC。
∴点P是线段AC的中点。
(2)在Rt△ABC中,AB=3,AC=4,∴ 。
。
∴ 。
。
由(1)∠PMC=∠C,∴sin∠PMC= 。
。

∵直线AC和PM分别与⊙O相切于点A,M,
∴PM=PA,OM⊥BC,BA⊥AC。
∴∠OMP=90°,∠BAC=90°。
∴∠1+∠2=90°,∠B+∠C=90°。
∵OB=OM,∴∠2=∠B。∴∠1=∠C。∴PC=PM。
又∵直线AC和PM分别与⊙O相切于点A,M,
∴PA=PM。∴PA=PC。
∴点P是线段AC的中点。
(2)在Rt△ABC中,AB=3,AC=4,∴
 。
。∴
 。
。由(1)∠PMC=∠C,∴sin∠PMC=
 。
。试题分析:(1)连接OM,根据切线的性质得OM⊥BC,BA⊥AC,根据切线长定理得PM=PA,则∠1+∠2=90°,∠B+∠C=90°,而∠2=∠B,所以∠1=∠C,于是得到PC=PM,则PA=PC。
(2)由于∠PMC=∠C,在Rt△ABC中,先根据勾股定理计算出BC=5,然后根据正弦的定义得到
 ,于是得到sin∠PMC的值。
,于是得到sin∠PMC的值。 
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
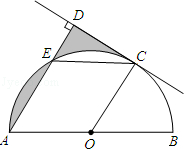
 的中点,⊙O的半径为1,求图中阴影部分的面积.
的中点,⊙O的半径为1,求图中阴影部分的面积.
 ,点E在AB上,且与A、B两点均不重合,点M在AD上,且ME=MD,过点E作EF⊥ME,交BC于点F,连接DE、MF.
,点E在AB上,且与A、B两点均不重合,点M在AD上,且ME=MD,过点E作EF⊥ME,交BC于点F,连接DE、MF.
 时,求MF的长;
时,求MF的长;


