Question

【题目】在边长为10的等边中，点从点出发沿射线移动，同时点从点出发沿线段的延长线移动，点、移动的速度相同， 与直线相交于点.

（1）如图①，当点为的中点时，

（I）求证： ；（II）求的长；

（2）如图②，过点作直线的垂线，垂足为，当点、在移动的过程中，试确定的数量关系，并说明理由.

Answer 1

【答案】（1）（I） （II）；（2）见解析

【解析】试题分析：

（1）I、过点P作PF∥AC交BC于点E，结合已知条件易证△PBF是等边三角形，从而可得PF=BP=CQ，由此易证△PFD≌△QCD，即可得到PD=QD；II、由△PFD≌△QCD可得DF=DC；由△PBF是等边三角形，点P是AB的中点可得BF=BP=5，由此可得FC=BC-BF=5，从而可得DC=CF=；

（2）由点P在射线BA上移动可知，需分点P在线段AB上和点P在线段AB的延长线上两种情况讨论：I、当点P在线段AB上时，如图②，由△PFD≌△QCD可得DF=DC；由△BPF是等边三角形，PE⊥BC于点E可得BE=FE；结合BF+FC即可得到2BE+2DC=BC，从而可得BE+DC=BC=；II、当点P在BA的延长线上时，如图③，过点P作过点P作PG∥AQ交BC的延长线于点G，易证△PGD≌△QCD，这样同理可得：此时BE-CD=BC=5.

试题解析：

（1）（I）如图①，过点P作PF∥AC交BC于点E，

∴，

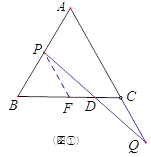
∴△是等边三角形，

∴，

又∵的运动速度相同，且同时出发，

∴，

∴，

又∵∠PDF=∠QDC，

∴△PFD≌△QCD，

∴PD=QD；

（II）∵P是AB的中点，△PBF是等边三角形，

∴BP=BF=5，

∴CF=10-BF=5，

由（I）可知△PFD≌△QCD，

∴DF=DC=CF=；

（2）如图②，

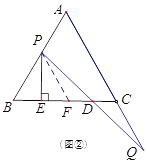
当点P在线段BA上时， =5，理由如下：

由（I）可知：△PFD≌△QCD，

∴DF=DC，

∵PE⊥BF，

∴BE=EF，

∵BF+CF=BC，

∴2BE+2CD=BC=10，

∴BE+CD=5，即BE+CD=BC=5；

如图③，当点P在线段BA的延长线上时， =5，理由如下：

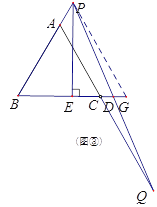
过点P作PG∥AQ交BC的延长线于点G，则∠G=∠DCQ=∠ACB=∠B=60°，∠GPD=∠CQD，

∴PG=BP，

∵点P、Q同时出发，且速度相同，

∴DQ=BP，

∴PG=QD，

∴△PGD≌△QCD，

∴DC=DG，即CG=2DC，

∵PG=PB，PE⊥BC于点E，

∴BE=GE，即BG=2BE，

∵BG-CG=BC，

∴2BE-2CD=BC，

∴BE-CD=BC=5.