题目内容
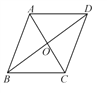
【题目】已知如图所示，△AOB与△COD关于点O成中心对称，连接BC，AD.
(1)求证：四边形ABCD为平行四边形；
(2)若△AOB的面积为15 cm2，求四边形ABCD的面积.
【答案】（1）证明见解析；（2）60 cm2.
【解析】试题分析：根据成中心对称图形的性质知OA=OC，OB=OD.根据平行四边形对角线互相平分，所以可以得到四边形ABCD为平行四边形；△AOB的面积为15 cm2，则△ABC面积等于△AOB面积的2倍，因为点O为平行四边形的中心，所以△ABC的高等于△AOB高的2倍，所以S△ABC =30，所以四边形ABCD的面积是60.
(1)∵AOB与△COD关于点O成中心对称，∴OA=OC，OB=OD.
∴四边形ABCD为平行四边形.
(2)四边形ABCD的面积为60 cm2.
练习册系列答案
相关题目
