题目内容
【题目】如图,已知线段AB=a,点C在直线AB上,![]() .
.
(1)用尺规作图画出点C;
(2)若点P在线段BC上,且BP:PC=2:3,D为线段PC的中点,求BD的长(用含a的代数式表示);
(3)在(2)的条件下,若AD=3cm,求a的值.
【答案】(1)详见解析;(2)![]() 或
或![]() ;(3)
;(3)![]() 或
或![]() .
.
【解析】
试题分析:(1)分两种情况画图:点C在线段AB的延长线上或C点在线段AB的反向延长线上;
(2)对于图1,BC=2a,由BP:PC=2:3可计算出BP=![]() BC=
BC=![]() a,PC=
a,PC=![]() BC=
BC=![]() a,再由D为线段PC的中点得到PD=
a,再由D为线段PC的中点得到PD=![]() PC=
PC=![]() a,然后利用BD=BP+PD计算得BD=
a,然后利用BD=BP+PD计算得BD=![]() a;对于图2,BC=4a,由BP:PC=2:3可计算得BP=
a;对于图2,BC=4a,由BP:PC=2:3可计算得BP=![]() BC=
BC=![]() a,PC=
a,PC=![]() BC=
BC=![]() a,再由D为线段PC的中点得到PD=
a,再由D为线段PC的中点得到PD=![]() PC=
PC=![]() a,然后利用BD=BP+PD计算可得BD=
a,然后利用BD=BP+PD计算可得BD=![]() a;(3)对于图1,先得到CD=PD=
a;(3)对于图1,先得到CD=PD=![]() a,再计算出AD=AC-CD=
a,再计算出AD=AC-CD=![]() a,则
a,则![]() a=3,然后解方程即可;对于图2,先得到CD=PD=
a=3,然后解方程即可;对于图2,先得到CD=PD=![]() a,利用计算出AD=BC-CD=
a,利用计算出AD=BC-CD=![]() a,则
a,则![]() a=3,然后解方程即可.
a=3,然后解方程即可.
试题解析::解:(1)如图所示:当点C在线段AB的延长线上,如图1:
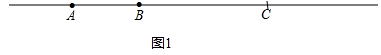
当C点在线段AB的反向延长线上时,如图2:
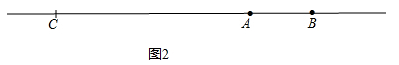 ;
;
(2)对于图1,
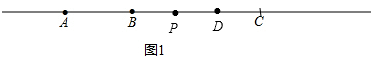
∵AB=a,∴AC=3a,∴BC=2a,
∵BP:PC=2:3,∴BP=![]() BC=
BC=![]() 2a=
2a=![]() a,PC=
a,PC=![]() BC=
BC=![]() a,
a,
∵D为线段PC的中点,∴PD=![]() PC=
PC=![]() a,
a,
∴BD=BP+PD=![]() a+
a+![]() a=
a=![]() a;
a;
对于图2,

BC=AB+AC=4a,
∵BP:PC=2:3,∴BP=![]() BC=
BC=![]() 4a=
4a=![]() a,PC=
a,PC=![]() BC=
BC=![]() a,
a,
∵D为线段PC的中点,∴PD=![]() PC=
PC=![]() a,∴BD=BP+PD=
a,∴BD=BP+PD=![]() a+
a+![]() a=
a=![]() a;
a;
(3)对于图1,CD=PD=![]() a,AD=AC-CD=3a-
a,AD=AC-CD=3a-![]() a=
a=![]() a=3,解得a=
a=3,解得a=![]() (cm);
(cm);
对于图2,CD=PD=![]() a,AD=BC-CD=4a-
a,AD=BC-CD=4a-![]() a=
a=![]() a=3,解得a=
a=3,解得a=![]() (cm).
(cm).
考点:分类讨论;线段的计算;一元一次方程的应用.

