题目内容
如图,A、B为⊙O上的两个定点,P是⊙O上的动点(P不与A、B重合),我们称∠APB为⊙O上关于A、B的滑动角。
(1)已知∠APB是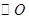 上关于点A、B的滑动角。
上关于点A、B的滑动角。
① 若AB为⊙O的直径,则∠APB=
② 若⊙O半径为1,AB=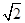 ,求∠APB的度数
,求∠APB的度数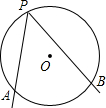
(2)已知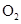 为
为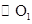 外一点,以
外一点,以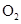 为圆心作一个圆与
为圆心作一个圆与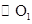 相交于A、B两点,∠APB为
相交于A、B两点,∠APB为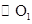 上关于点A、B的滑动角,直线PA、PB分别交
上关于点A、B的滑动角,直线PA、PB分别交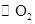 于点M、N(点M与点A、点N与点B均不重合),连接AN,试探索∠APB与∠MAN、∠ANB之间的数量关系。
于点M、N(点M与点A、点N与点B均不重合),连接AN,试探索∠APB与∠MAN、∠ANB之间的数量关系。
解:(1)①900。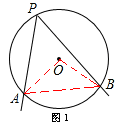
②如图,连接AB、OA、OB.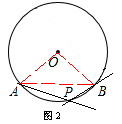
在△AOB中,∵OA=OB=1.AB= ,∴OA2+OB2=AB2。
,∴OA2+OB2=AB2。
∴∠AOB=90°。
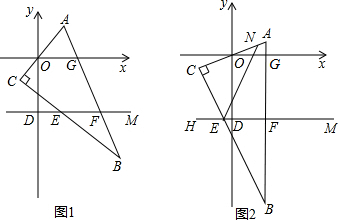
当点P在优弧 AB 上时(如图1),∠APB=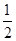 ∠AOB=45°;
∠AOB=45°;
当点P在劣弧 AB 上时(如图2),
∠APB=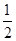 (360°-∠AOB)=135°。
(360°-∠AOB)=135°。
(2)根据点P在⊙O1上的位置分为以下四种情况.
第一种情况:点P在⊙O2外,且点A在点P与点M之间,点B在点P与点N之间,如图3,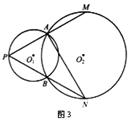
∵∠MAN=∠APB+∠ANB,
∴∠APB=∠MAN-∠ANB。
第二种情况:点P在⊙O2外,且点A在点P与点M之间,点N在点P与点B之间,如图4,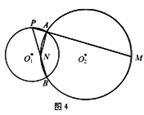
∵∠MAN=∠APB+∠ANP=∠APB+(180°-∠ANB),
∴∠APB=∠MAN+∠ANB-180°。
第三种情况:点P在⊙O2外,且点M在点P与点A之间,点B在点P与点N之间,如图5,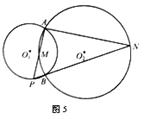
∵∠APB+∠ANB+∠MAN=180°,
∴∠APB=180°-∠MAN-∠ANB。
第四种情况:点P在⊙O2内,如图6,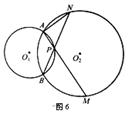
∠APB=∠MAN+∠ANB。
解析

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
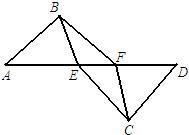 24、如图,E、F为AD上两点,且AF=DE,AB=DC,BE=CF.
24、如图,E、F为AD上两点,且AF=DE,AB=DC,BE=CF.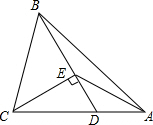 如图,△ABC中D为AC上一点,CD=2DA,∠BAC=45°,∠BDC=60°,CE⊥BD,E为垂足,连接AE.
如图,△ABC中D为AC上一点,CD=2DA,∠BAC=45°,∠BDC=60°,CE⊥BD,E为垂足,连接AE.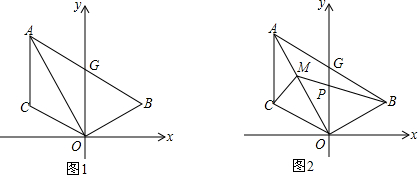
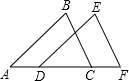 如图,D、C为AF上两点,AD=CF,AB=DE,要使得△ABC≌△DEF,需补充边的条件为
如图,D、C为AF上两点,AD=CF,AB=DE,要使得△ABC≌△DEF,需补充边的条件为