题目内容
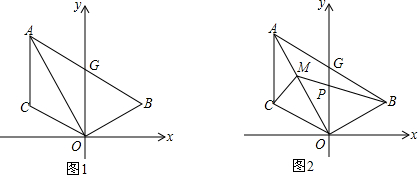
如图1,已知线段AC∥y轴,点B在第一象限,且AO平分∠BAC,AB交y轴与G,连OB、OC.
(1)判断△AOG的形状,并予以证明;
(2)若点B、C关于y轴对称,求证:AO⊥BO;
(3)在(2)的条件下,如图2,点M为OA上一点,且∠ACM=45°,BM交y轴于P,若点B的坐标为(3,1),求点M的坐标.
(1)判断△AOG的形状,并予以证明;
(2)若点B、C关于y轴对称,求证:AO⊥BO;
(3)在(2)的条件下,如图2,点M为OA上一点,且∠ACM=45°,BM交y轴于P,若点B的坐标为(3,1),求点M的坐标.

分析:(1)△AOG的形状是等腰三角形,利用已知条件证明AG=OG即可;
(2)接连BC,易证△COD≌△BOE(HL),设∠BAO=∠CAO=x,∠OBC=∠OCB=y,利用全等三角形的性质和已知条件证明∠AOB=∠ACB=90°,即可得到AO⊥BO;
(3)连BC,作MG⊥x轴于G,BH⊥x轴于H,易证△OMG≌△OBH,OG=BH=1,MG=OH=3,所以M(-1,3).
(2)接连BC,易证△COD≌△BOE(HL),设∠BAO=∠CAO=x,∠OBC=∠OCB=y,利用全等三角形的性质和已知条件证明∠AOB=∠ACB=90°,即可得到AO⊥BO;
(3)连BC,作MG⊥x轴于G,BH⊥x轴于H,易证△OMG≌△OBH,OG=BH=1,MG=OH=3,所以M(-1,3).
解答:解:(1)△AOG的形状是等腰三角形,
理由如下:
∵AC∥y轴,
∴∠CAO=∠GOA,
∵AO平分∠BAC,
∴∠CAO=∠GAO,
∴∠GOA=∠GAO,
∴AG=OG,
∴△AOG是等腰三角形;
(2)接连BC,过O作OE⊥AB于E,
∵B、C关于y轴对称,AC∥y轴,
∴AC⊥BC,
在Rt△COD和Rt△BOE中,
,
∴△COD≌△BOE(HL),
∴∠DCO=∠EBO,
∴∠BAC+∠BOC=180°,
设∠BAO=∠CAO=x,∠OBC=∠OCB=y,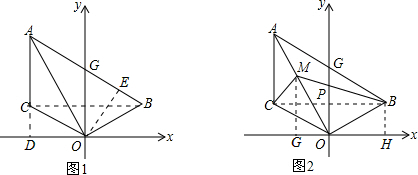
∴2x+∠BOC=180°,
又∵2y+∠BOC=180°,
∴x=y,故∠OAC=∠OBC,
∴∠AOB=∠ACB=90°,
∴AO⊥OB;
(3)连BC,作MG⊥x轴于G,BH⊥x轴于H,
则∠ACB=90°,
∵∠ACM=45°,
∴CM平分∠ACB,又AM平分∠BAC,
∴BM平分∠ABC,设∠ABM=∠CBM=z,
由(2)可得∠OMB=x+z,∠OBM=y+z=x+z
∴∠OMB=∠OBM,
∴OM=OB
∴△OBM为等腰直角三角形,
,
∴△OMG≌△OBH(AAS),
∴OG=BH=1,MG=OH=3,
∴M(-1,3).
理由如下:
∵AC∥y轴,
∴∠CAO=∠GOA,
∵AO平分∠BAC,
∴∠CAO=∠GAO,
∴∠GOA=∠GAO,
∴AG=OG,
∴△AOG是等腰三角形;
(2)接连BC,过O作OE⊥AB于E,
∵B、C关于y轴对称,AC∥y轴,
∴AC⊥BC,
在Rt△COD和Rt△BOE中,
|
∴△COD≌△BOE(HL),
∴∠DCO=∠EBO,
∴∠BAC+∠BOC=180°,
设∠BAO=∠CAO=x,∠OBC=∠OCB=y,

∴2x+∠BOC=180°,
又∵2y+∠BOC=180°,
∴x=y,故∠OAC=∠OBC,
∴∠AOB=∠ACB=90°,
∴AO⊥OB;
(3)连BC,作MG⊥x轴于G,BH⊥x轴于H,
则∠ACB=90°,
∵∠ACM=45°,
∴CM平分∠ACB,又AM平分∠BAC,
∴BM平分∠ABC,设∠ABM=∠CBM=z,
由(2)可得∠OMB=x+z,∠OBM=y+z=x+z
∴∠OMB=∠OBM,
∴OM=OB
∴△OBM为等腰直角三角形,
|
∴△OMG≌△OBH(AAS),
∴OG=BH=1,MG=OH=3,
∴M(-1,3).
点评:本题考查了角平分线的性质、轴对称的性质、全等三角形的判定和性质、等腰三角形的判定和性质、三角形的内角和定理,题目的综合性强、需要添加的辅助线比较多,是此题的特点.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
 18、
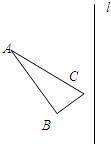
18、 作图题:
作图题: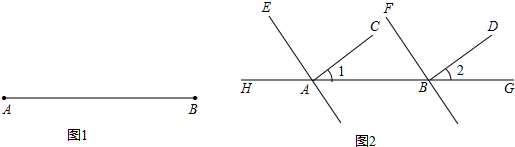
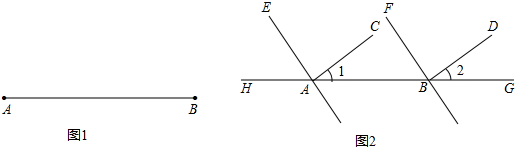
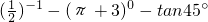 .
.
 .
.