题目内容
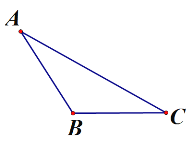
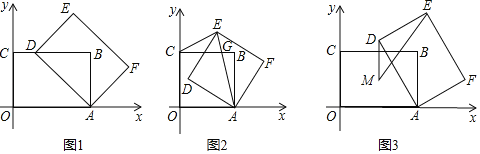
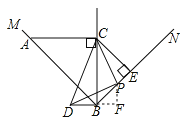
【题目】如图，∠MBN=90°，点C是∠MBN平分线上的一点，过点C分别作AC⊥BC，CE⊥BN，垂足分别为点C，E，AC=
，点P为线段BE上的一点（点P不与点B、E重合），连接CP，以CP为直角边，点P为直角顶点，作等腰直角三角形CPD，点D落在BC左侧．
（1）求证：
；
（2）连接BD，请你判断AC与BD的位置关系，并说明理由；
（3）设PE=x，△PBD的面积为S，求S与x之间的函数关系式．
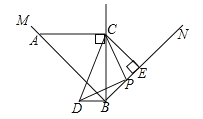
【答案】（1）证明见解析；（2）AC∥BD；（3）
．
【解析】
试题（1）由△CPD∽△CEB证得结论；
（2）AC∥BD．欲推知AC∥BD，直线推知∠ACB+∠DBC=180°；
（3）如图所示，过点P作PF⊥BD．交DB的延长线于点F．通过解直角三角形、（2）中相似三角形的对应边成比例和三角形的面积公式写出函数关系式即可．
试题解析：（1）证明：∵∠MBN=90°，点C是∠MBN平分线上的一点，∴∠CBE=45°，又CE⊥BN，∴∠BCE=45°，∴BE=CE，∴△BCE是等腰直角三角形．
又∵△CPD是等腰直角三角形，∴△CPD∽△CEB，∴
，∴
；
（2）解：AC∥BD，理由如下：
∵∠PCE+∠BCP=∠DCB+∠BCP=45°，∴∠PEC=∠DCB．
由（1）知，，∴△EPC∽△BDC，∴∠PEC=∠DBC．
∵AC⊥BC，∴∠ACB=90°，∴∠ACB+∠DBC=180°，∴AC∥BD；
（3）解：如图所示，过点P作PF⊥BD．交DB的延长线于点F．
∵AC=
，△ABC与△BEC都是等腰直角三角形，∴BC=，BE=CE=4．
由（2）知，△EPC∽△BDC，∴
．即
，∴DB=
x．
∵∠PBF=∠CBF﹣∠CBP=90°﹣45°=45°，即BP=BE﹣PE=4﹣x，∴PF=BPsin∠PBF=（4﹣x）×
=
﹣x，∴S=
DBPF=×x×（﹣x），即：．
