题目内容
【题目】矩形ABCO,O(0,0),C(0.3),A(a.0),(a≥3),以A为旋转中心顺时针旋转矩形ABCO,得到矩形AFED.
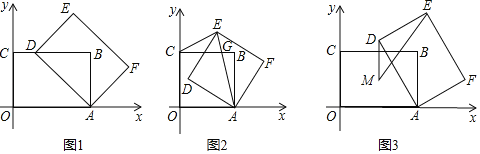
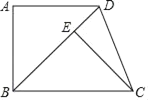
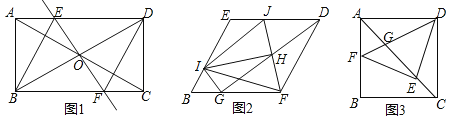
(1)如图1,当点D落在边BC上时,求BD的长;
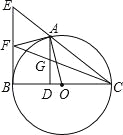
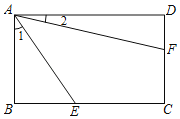
(2)如图2,当a=3时,矩形AFEO的对角线A任交矩形ABCO的边BC于点G,连结CE.若△CGE是等腰三角形,求直线BE的解析式.
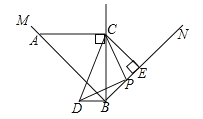
(3)如图3,当a=4时,矩形ABCD的对称中心为点M,△MED的面积为s,求s的取值范围.
【答案】(1)![]() ;(2)y=﹣x+6;(3)
;(2)y=﹣x+6;(3)![]()
【解析】
(1)如图1,当点D落在边BC上时,BD2=AD2﹣AB2,即可求解;
(2)分CG=EG、CE=GE、CE=CG三种情况分别求解;
(3)MN≤MA+AD,当射线DA经过点M时,MN=MA+AD=![]() ,当边AD经过点M,即P与M重合时,MN=PD,MN=PD=AD﹣AP=4-
,当边AD经过点M,即P与M重合时,MN=PD,MN=PD=AD﹣AP=4-![]() ,即可求解.
,即可求解.
(1)如图1,
在矩形ABCO中,∠B=90°
当点D落在边BC上时,BD2=AD2﹣AB2,
∵C(0,3),A(a,0)
∴AB=OC=3,AD=AO=a,
∴BD=![]() ;
;
(2)如图2,连结AC,
∵a=3,∴OA=OC=3,
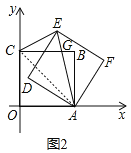
∴矩形ABCO是正方形,∴∠BCA=45°,
设∠ECG的度数为x,
∴AE=AC,∴∠AEC=∠ACE=45°+x,
①当CG=EG时,x=45°+x,
解得x=0,不合题意,舍去;
②当CE=GE时,如图2,
∠ECG=∠EGC=x
∵∠ECG+∠EGC+∠CEG=180°,
∴x+x+(45°+x)=180°,解得x=45°,
∴∠AEC=∠ACE=90°,不合题意,舍去;
③当CE=CG时,∠CEG=∠CGE=45°+x,
∵∠ECG+∠EGC+∠CEG=180°,
∴x+(45°+x)+(45°+x)=180°,解得x=30°,
∴∠AEC=∠ACE=75°,∠CAE=30°
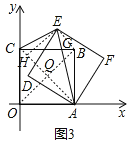
如图3,连结OB,交AC于点Q,过E作EH⊥AC于H,连结BE,
∴EH=![]() AE=
AE=![]() AC,BQ=
AC,BQ=![]() AC,
AC,
∴EH=BQ,EH∥BQ且∠EHQ=90°
∴四边形EHQB是矩形
∴BE∥AC,
设直线BE的解析式为y=﹣x+b,
∵点B(3,3)在直线上,则b=6,
∴直线BE的解析式为y=﹣x+6;
(3)如图4,
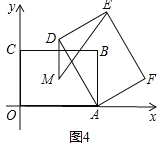
∵a=4,点M是矩形ABCO的对称中心
∴AO=4,AM=![]() ,
,
以A为圆心,分别以AO、AM为半径作圆,AD交小圆于P,
过M作MN⊥ED于N
∴DE切大圆于D
∴MN≥PD
根据“垂线段最短”,MN≤MA+AD,
如图5,当射线DA经过点M时,MN=MA+AD=![]() ,
,
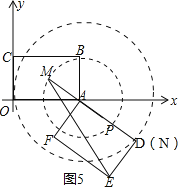
∴s的最大值是![]() ED×(MA+AD)=
ED×(MA+AD)=![]() ;
;
如图6,当边AD经过点M,即P与M重合时,MN=PD,
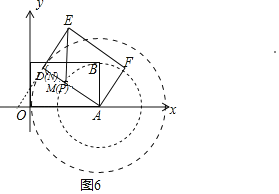
MN=PD=AD﹣AP=4﹣![]() =
=![]() ,
,
∴s的最小值是![]() ED×PD=
ED×PD=![]() ,
,
s的取值范围是![]()