题目内容
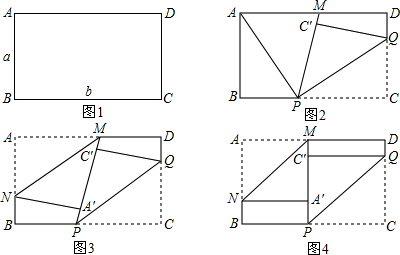
如图1,矩形纸片ABCD的边长分别为a,b(a<b).将纸片任意翻折(如图2),折痕为PQ.(P在BC上),使顶点C落在四边形APCD内一点C′,PC′的延长线交直线AD于M,再将纸片的另一部分翻折,使A落在直线PM上一点A′,且A′M所在直线与PM所在直线重合(如图3)折痕为MN.(1)猜想两折痕PQ,MN之间的位置关系,并加以证明;
(2)若∠QPC的角度在每次翻折的过程中保持不变,则每次翻折后,两折痕PQ,MN间的距离有何变化?请说明理由;
(3)若∠QPC的角度在每次翻折的过程中都为45°(如图4),每次翻折后,非重叠部分的四边形MC′QD,及四边形BPA′N的周长与a,b有何关系,为什么?
分析:(1)猜想两直线平行,由矩形的对边平行,得到一组内错角相等,翻折前后对应角相等,那么可得到PQ与MN被MP所截得的内错角相等,得到平行.
(2)作出两直线间的距离.∵PM长相等,∠NPM是不变的,所以利用相应的三角函数可得到两直线间的距离不变.
(3)由特殊角得到所求四边形的形状,把与周长相关的边转移到同一线段求解.
(2)作出两直线间的距离.∵PM长相等,∠NPM是不变的,所以利用相应的三角函数可得到两直线间的距离不变.
(3)由特殊角得到所求四边形的形状,把与周长相关的边转移到同一线段求解.
解答:解:(1)PQ∥MN.
∵四边形ABCD是矩形,∴AD∥BC,且M在AD直线上,则有AM∥BC.
∴∠AMP=∠MPC.
由翻折可得:∠MPQ=∠CPQ=
∠MPC,
∠NMP=∠AMN=
∠AMP,
∴∠MPQ=∠NMP,故PQ∥MN.
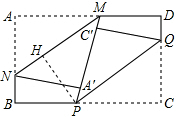
(2)两折痕PQ,MN间的距离不变.
过P作PH⊥MN,则PH=PM•sin∠PMH,
∵∠QPC的角度不变,
∴∠C'PC的角度也不变,则所有的PM都是平行的.
又∵AD∥BC,
∴所有的PM都是相等的.
又∵∠PMH=∠QPC,故PH的长不变.
(3)当∠QPC=45°时,
四边形PCQC'是正方形,
四边形C'QDM是矩形.
∵C'Q=CQ,C'Q+QD=a,
∴矩形C'QDM的周长为2a.
同理可得矩形BPA'N的周长为2a,∴两个四边形的周长都为2a,与b无关.
∵四边形ABCD是矩形,∴AD∥BC,且M在AD直线上,则有AM∥BC.
∴∠AMP=∠MPC.
由翻折可得:∠MPQ=∠CPQ=
| 1 |
| 2 |
∠NMP=∠AMN=
| 1 |
| 2 |
∴∠MPQ=∠NMP,故PQ∥MN.

(2)两折痕PQ,MN间的距离不变.
过P作PH⊥MN,则PH=PM•sin∠PMH,
∵∠QPC的角度不变,
∴∠C'PC的角度也不变,则所有的PM都是平行的.
又∵AD∥BC,
∴所有的PM都是相等的.
又∵∠PMH=∠QPC,故PH的长不变.
(3)当∠QPC=45°时,
四边形PCQC'是正方形,
四边形C'QDM是矩形.
∵C'Q=CQ,C'Q+QD=a,
∴矩形C'QDM的周长为2a.
同理可得矩形BPA'N的周长为2a,∴两个四边形的周长都为2a,与b无关.
点评:翻折前后对应角相等,对应边相等,应注意使用相应的三角函数,平行线的判断,特殊四边形的判定.

练习册系列答案
相关题目
 13、如图,将矩形纸片ABCD沿对角线AC折叠,使点B落到点B′的位置,AB′与CD交于点E.
13、如图,将矩形纸片ABCD沿对角线AC折叠,使点B落到点B′的位置,AB′与CD交于点E. (2013•松北区三模)如图,将矩形纸片ABCD折痕,使点D落在点线段AB的中点F处.若AB=4,则边BC的长为( )
(2013•松北区三模)如图,将矩形纸片ABCD折痕,使点D落在点线段AB的中点F处.若AB=4,则边BC的长为( ) 如图,把矩形纸片ABCD沿折叠,使点B落在边AD上的点B′处,点A落在点A′处;
如图,把矩形纸片ABCD沿折叠,使点B落在边AD上的点B′处,点A落在点A′处; 17、如图,将矩形纸片ABCD沿EF折叠,点C与点A重合,点D落在点D′处,已知AB=4,BC=8,则线段AE的长度是
17、如图,将矩形纸片ABCD沿EF折叠,点C与点A重合,点D落在点D′处,已知AB=4,BC=8,则线段AE的长度是
