Question

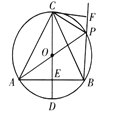
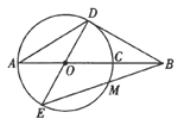
【题目】如图，线段AB经过⊙O的圆心，交⊙O于A,C两点，为⊙O的弦，连接BD, ，连接DO并延长交⊙O于点E，连接BE交⊙O 于点M .

(1)求证:直线BD是⊙O的切线;

(2)求切线BD的长;

(3)求线段BM的长.

Answer 1

【答案】（1）详见解析；（2）；（3）.

【解析】

（1）由，得：∠ADB=120°，由OA=OD，∠OAD=∠ODA=30°，进而可得：OD⊥BD，即可得到结论；

（2）设OC=OD=x，由OB=2OD，列出方程，即可得到答案；

（3）连接DM，易证：DBM~EBD，从而得：，结合，即可求解.

（1）∵，

∴∠ADB=180°-30°-30°=120°，

∵OA=OD，

∴∠OAD=∠ODA=30°，

∴∠ODB=∠ADB-∠ODA=120°-30°=90°，

即：OD⊥BD，

∴直线BD是⊙O的切线；

（2）设OC=OD=x，

∵在RtOBD中，∠ABD=30°，

∴OB=2OD，即：x+1=2x，解得：x=1，

∴OD=1，OB=2，

∴BD=；

（3）连接DM，

∵在RtBDE中，BD=，BE=2OD=2，

∴，

∵DE是直径，

∴∠DME=90°，

∴∠BDM=90°-∠EBD=∠E，

∵∠DBM=∠EBD，

∴DBM~EBD，

∴，即：，

∴BM=.