题目内容
16、已知二次函数y=x2-4x+3（1）用配方法将y=x2-4x+3化成y=a（x-h）2+k的形式；
（2）在所给的平面直角坐标系中，画出这个二次函数的图象；
（3）根据图象回答：当自变量x的取值范围满足什么条件时，y＜0？
分析：（1）根据二次完全平方公式（a+b）2=a2+2ab+b2来解答；
（2）根据（1）中所求的二次函数的顶点式解析式作图；
（3）根据（2）中的函数图象很直观的得出答案．
（2）根据（1）中所求的二次函数的顶点式解析式作图；
（3）根据（2）中的函数图象很直观的得出答案．
解答：解：（1）y=x2-4x+3
=x2一4x+4-4+3
=（x一2）2-1；
（2）根据（1）中的二次函数的顶点式关系式可知，该函数的顶点是（2，-1）；
当x=0时，y=3；
当y=0时，即x2-4x+3=0，解得x=1或x=3，
∴该函数图象经过点（0，3）、（1，0）、（3，0）；
所以二次函数y=x2-4x+3的图象如图所示：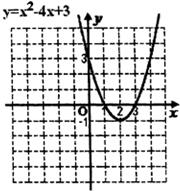
（3）由（2）中的图象可知，当1＜x＜3时，y＜0．
=x2一4x+4-4+3
=（x一2）2-1；
（2）根据（1）中的二次函数的顶点式关系式可知，该函数的顶点是（2，-1）；
当x=0时，y=3；
当y=0时，即x2-4x+3=0，解得x=1或x=3，
∴该函数图象经过点（0，3）、（1，0）、（3，0）；
所以二次函数y=x2-4x+3的图象如图所示：
（3）由（2）中的图象可知，当1＜x＜3时，y＜0．
点评：本题主要考查的是二次函数的顶点式解析式、二次函数的图象及其单调性．
练习册系列答案
导学全程练创优训练系列答案
相关题目
已知二次函数y=x2+（2a+1）x+a2-1的最小值为0，则a的值是（ ）
A、
| ||
B、-
| ||
C、
| ||
D、-
|
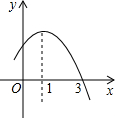已知二次函数y=-x2+2x+m的部分图象如图所示，则关于x的一元二次方程-x2+2x+m=0的解为（ ）| A、x1=1，x2=3 | B、x1=0，x2=3 | C、x1=-1，x2=1 | D、x1=-1，x2=3 |
已知二次函数y=-x2+bx+c的图象如图所示，它与x轴的一个交点坐标为（-1，0），与y轴的交点坐标为（0，3）．