题目内容
 如图,已知AD∥BC.
如图,已知AD∥BC.(1)找出图中所有面积相等的三角形,并选择其中一对说明理由;
(2)如果BE⊥AC,CF⊥BD,垂足分别为E、F,
| AC |
| BD |
| 3 |
| 4 |
| BE |
| CF |
分析:(1)根据等底等高的三角形的面积相等解答;
(2)利用△ABC和△BCD的面积列式整理即可得解.
(2)利用△ABC和△BCD的面积列式整理即可得解.
解答:解:(1)①△ABC与△BCD,②△ADB与△ADC,③△AMB与△DMC;
选择①说明:设AD、BC间的距离为h,
则S△ABC=
BC•h,S△BCD=
BC•h,
∴△ABC与△DBC的面积相等;
(2)∵S△ABC=S△BCD,
∴
AC•BE=
BD•CF,
∴
=
,
∵
=
,
∴
=
.
选择①说明:设AD、BC间的距离为h,
则S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
∴△ABC与△DBC的面积相等;
(2)∵S△ABC=S△BCD,
∴
| 1 |
| 2 |
| 1 |
| 2 |
∴
| BE |
| CF |
| BD |
| AC |
∵
| AC |
| BD |
| 3 |
| 4 |
∴
| BE |
| CF |
| 4 |
| 3 |
点评:本题考查了三角形的面积,平行线间的距离相等,熟记等底等高的三角形的面积相等是解题的关键.

练习册系列答案
相关题目
 9、如图,已知AD∥BC,∠1=∠2,∠A=112°,且BD⊥CD,则∠ABC=
9、如图,已知AD∥BC,∠1=∠2,∠A=112°,且BD⊥CD,则∠ABC= 如图,已知AD=BC.EC⊥AB.DF⊥AB,C.D为垂足,要使△AFD≌△BEC,还需添加一个条件.若以“ASA”为依据,则添加的条件是
如图,已知AD=BC.EC⊥AB.DF⊥AB,C.D为垂足,要使△AFD≌△BEC,还需添加一个条件.若以“ASA”为依据,则添加的条件是 如图,已知AD=BC,AC=BD,∠DAC与∠CBD有什么关系?说说你的理由.
如图,已知AD=BC,AC=BD,∠DAC与∠CBD有什么关系?说说你的理由.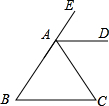 如图,已知AD∥BC,AD平分∠CAE,试说明△ABC是等腰三角形.
如图,已知AD∥BC,AD平分∠CAE,试说明△ABC是等腰三角形. 如图,已知AD∥BC,∠1=∠2,∠A=112°,且BD⊥CD,则∠C=
如图,已知AD∥BC,∠1=∠2,∠A=112°,且BD⊥CD,则∠C=