题目内容
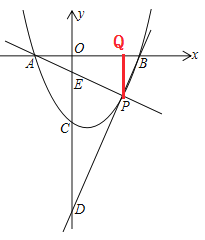
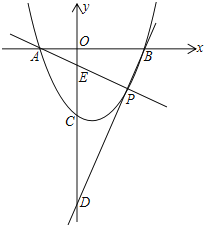
【题目】如图,已知抛物线y=x2-(2m+1)x+m2+m-2与x轴交于A、B两点,点A在点B的左边,与y轴交于点C,P(s,t)为抛物线上A、B之间一点(不包括A、B),连接AP、BP分别交y轴于点E、D
(1)若m=-1,求A、B两点的坐标
(2)若s=1,求ED的长度
(3)若∠BAP=∠ODP,求t的值
【答案】(1)A(-2,0)、B(1,0)(2)3(3) t=-1
【解析】试题分析:(1)把m=-1代入抛物线y=x2-(2m+1)x+m2+m-2得y=x2+x-2,令y=0得方程x2+x-2=0,解得x=-2或x=1,即可得)A(-2,0)、B(1,0);(2)先求得A、B两点的坐标,再表示出点P的坐标,分别求得直线AP、BP的解析式,从而求得DE的长;(3)由∠BAP=∠ODP可得∠DPE=∠AOE=90°,过点P作PQ⊥x轴于Q,由射影定理得,t2=(s-xA)(xB-s),整理得s(xA+xB)-s2-xAxB=t2,根据根与系数的关系可得s·(2m+1)-s2-(m-1)(m+2)=t2,把x=s代入解得t值即可.
试题解析:
(1)A(-2,0)、B(1,0)
(2)∵y=[x-(m+2)][x-(m-1)]
∴A(m-1,0)、B(m+2,0)
∵s=1
∴P(1,m2-m-2)
∴直线AP的解析式为y=-(m+1)x+m2-1
直线BP的解析式为y=-(m-2)x+m2-4
∴DE=m2-1-(m2-4)=3
(3) ∵∠BAP=∠ODP
∴∠DPE=∠AOE=90°
过点P作PQ⊥x轴于Q
由射影定理得,t2=(s-xA)(xB-s)
∴s(xA+xB)-s2-xAxB=t2
∴s·(2m+1)-s2-(m-1)(m+2)=t2
当x=s时,t=s2-(2m+1)s+(m-1)(m+2)
∴t2=-t,解得t=-1