题目内容
【题目】图6, ![]() ,给出下列结论:①
,给出下列结论:① ![]() 1=
1= ![]() 2;②BE=CF;③CD=DN;④△CAN
2;②BE=CF;③CD=DN;④△CAN ![]() △ABM.其中正确的结论是( )
△ABM.其中正确的结论是( )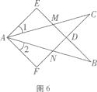
A.①③
B.②
C.②③
D.①②④
【答案】D
【解析】解 :在△AEB与△AFC中,
∵∠E=∠F=90,∠B=∠C,AE=AF,
∴△AEB≌△AFC(AAS),
∴BE=CF,∠EAB=∠FAC,
∴∠1+∠CAB=∠2+∠CAB
∴∠1=∠2,
故①②正确;
∵△AEB≌△AFC
∴AC=AB
又∵∠CAB=∠CAB,∠B=∠C
∴△ACN≌△BAM(ASA),
故④是正确的;
∵△ACN≌△BAM,
∴AM=AN,
又∵AC=AB
∴CM=BN,
又∵∠B=∠C,∠CDM=∠BDN,
∴△CDM≌△BDN,
∴CD=BD,
而DN与BD不一定相等,因而CD=DN不一定成立,故③错误。
故应选 :D 。
根据E=∠F=90°,∠B=∠C,AE=AF利用AAS可以证得△AEB≌△AFC,根据全等三角形对应边相等,对应角相等得出BE=CF,∠EAB=∠FAC,根据等式的性质得出∠1=∠2,故①②正确;根据全等三角形对应边相等得出AC=AB,进而利用ASA证得△AEB≌△AFC,故④是正确的;根据全等三角形对应边相等得出AM=AN,进而得出CM=BN,然后利用AAS判断出△CDM≌△BDN从而作出判断.

练习册系列答案
相关题目