题目内容
（1997•新疆）已知：如图，⊙O1与⊙O2相交于A、B，点O2在⊙O1上，AD是⊙O2的直径，连接DB并延长交⊙O1于点C求证：
| 1 |
| 2 |
| CD2-CO22 |
分析：首先根据圆周角定理得出∠ABD=∠CO2D，进而得出∠ABD=90°=∠CO2D，再由勾股定理求出O2D即可得出答案．
解答：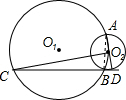
证明：连接AB，
在△BAD和△CO2D中
∵∠BAD=∠C，∠D=∠D，
∴∠ABD=∠CO2D，
∵AD是⊙O2直径，
∴∠ABD=90°=∠CO2D，
Rt△CO2D中，O2D=
，
又∵O2D=
AD，
∴
AD=
．
证明：连接AB，在△BAD和△CO2D中
∵∠BAD=∠C，∠D=∠D，
∴∠ABD=∠CO2D，
∵AD是⊙O2直径，
∴∠ABD=90°=∠CO2D，
Rt△CO2D中，O2D=
CD2-C
|
又∵O2D=
| 1 |
| 2 |
∴
| 1 |
| 2 |
CD2-C
|
点评：此题主要考查了圆周角定理以及勾股定理等知识，根据已知得出O2D=
是解题关键．
CD2-C
|
练习册系列答案
相关题目
（1997•新疆）已知抛物线经过一直线y=3x-3与x轴、y轴的交点，并经过（2，5）点．