Question

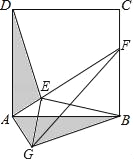
【题目】如图，点E是正方形ABCD内一点，点E到点A，B和D的距离分别为1，2，，将△ADE绕点A旋转至△ABG，连接AE，并延长AE与BC相交于点F，连接GF，则△BGF的面积为_____．

Answer 1

【答案】

【解析】

作BM⊥AF垂足为F，根据勾股定理逆定理得到△EGB是直角三角形，即可得到△BEM是等腰直角三角形，利用△ABM∽△AFB得到FM的长，进而得到AF=AE+ME+MF=，最后根据S△BGF=S△AEG+S△BEG+S△BEF-S△AFG进行计算即可．

如图，作BM⊥AF于点M，

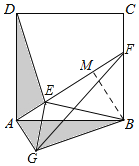
∵四边形ABCD为正方形，

∴AB=AD，∠BAD=90°，

∵△ADE绕点A顺时针旋转后得到△ABG，

∴△AED≌△AGB，∠EAG=90°，

∴AE=AG=1，BG=DE=，

∴GE=，

又∵BE=2，

∴EG2+EB2=10=BG2，

∴△BEG是直角三角形，∠BEG=90°，

∵∠AEG=∠AGE=45°，∠BEM+∠AEG=90°，

∴∠BEM=45°，

∵BE=2，

∴ME=MB=2，AM=AE+ME=1+2=3，

又可证△AMB∽△BMF，

∴，

∴FM=，

∴AF=AE+ME+MF=，

由图可得，S△BGF=S△AEG+S△BEG+S△BEF-S△AFG

=×1×1+××2+×（2+）×2-×1×

=．

故答案为：．