题目内容
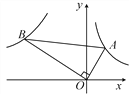
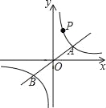
【题目】如图,已知双曲线y=![]() (m>0)与直线y=kx交于A、B两点,点A的坐标为(3,2).
(m>0)与直线y=kx交于A、B两点,点A的坐标为(3,2).
(1)由题意可得m的值为 ,k的值为 ,点B的坐标为 ;
(2)若点P(n﹣2,n+3)在第一象限的双曲线上,试求出n的值及点P的坐标;
(3)在(2)小题的条件下:如果M为x轴上一点,N为y轴上一点,以点P、A、M、N为顶点的四边形是平行四边形,试求出点M的坐标.
【答案】(1)6;![]() ;(﹣3,﹣2);(2)n=3,P(1,6);(3)M1(2,0);M2(﹣2,0).
;(﹣3,﹣2);(2)n=3,P(1,6);(3)M1(2,0);M2(﹣2,0).
【解析】
试题(1)把A坐标代入反比例解析式求出m的值,确定出反比例解析式,把A坐标代入直线解析式求出k的值,利用对称性求出B坐标即可;
(2)把P坐标代入反比例解析式求出n的值,确定出P坐标即可;
(3)分两种情况考虑:当M1在x轴正半轴,N1在y轴上半轴时,如图1所示;当M2在x轴负半轴,N2在y轴下半轴时,如图2所示,分别求出M坐标即可.
解:(1)把A(3,2)代入反比例解析式得:m=6;
把A(3,2)代入直线解析式得:k=![]() ,
,
由对称性得:B(﹣3,﹣2);
故答案为:6;![]() ;(﹣3,﹣2);
;(﹣3,﹣2);
(2)把P(n﹣2,n+3)代入y=![]() 中得:(n﹣2)(n+3)=6,
中得:(n﹣2)(n+3)=6,
整理得:n2+n﹣12=0,即(n﹣3)(n+4)=0,
解得:n=3或n=﹣4(舍去),
则P(1,6);
(3)分两种情况考虑:
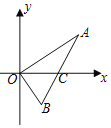
当M1在x轴正半轴,N1在y轴上半轴时,如图1所示,

过P作PQ∥y轴,过A作AQ∥x轴,交于点Q,
∵A(3,2),P(1,6),
∴AQ=3﹣1=2,
由平移及平行四边形性质得到OM1=2,即M1(2,0);
当M2在x轴负半轴,N2在y轴下半轴时,如图2所示,
同理得到OM2=2,即M2(﹣2,0).

 一线名师权威作业本系列答案
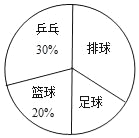
一线名师权威作业本系列答案【题目】某校为了调查八年级学生参加“乒乓”、“篮球”、“足球”、“排球”四项体育活动的人数,学校从八年级随机抽取了部分学生进行调查,根据调查结果制作了如下不完整的统计表、统计图:
类别 | 频数(人数) | 频率 |
乒乓 | a | 0.3 |
篮球 | 20 | |
足球 | 15 | b |
排球 | ||
合计 | c | 1 |
请你根据以上信息解答下列各题:
(1)a= ;b= ;c= ;
(2)在扇形统计图中,排球所对应的圆心角是 度;
(3)若该校八年级共有600名学生,试估计该校八年级喜欢足球的人数?.