题目内容
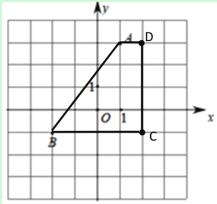
【题目】(1)如图1所示,写出A、B的坐标:A_________、B________;
(2)如图1所示,将点A向右平移1个单位到点D,点C、B关于y轴对称,求出四边形ABCD的面积;
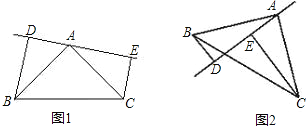
(3)将图1中的网格去掉得到图2所示,直线AB的交y轴于点C,直线CD⊥AB于点C,△ACD为等腰直角三角形,且∠ACD=90°,求点D的坐标.


【答案】(1)(1,3);(-2,-1);(2)10;(3)(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).
【解析】
(1)由平面直角坐标易写出A、B坐标;
(2)利用两坐标平移和对称的特点找出C、D的位置,再求四边形ABCD的面积即可.
(3)图中没有说明点D的位置,故需分类讨论:①若D点在第一象限,分别过点A、D作y轴的垂线交y轴于点E、F,利用一线三等角可证△ECA≌△FDC,在利用坐标关系求出点D坐标;②若D点在第二象限,原理同①.
解:(1)由平面直角坐标可知:A(1,3),B(-2,-1);
(2)将点A向右平移1个单位到点D,故D点坐标为(2,3),C、B关于y轴对称,故C点坐标为(2,-1),如下图所示:不难发现四边形ABCD为梯形,S梯形ABCD=![]() ;
;
(3)①若D点在第一象限,分别过点A、D作y轴的垂线交y轴于点E、F,如图所示,
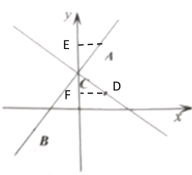
∵△ACD为等腰直角三角形
∴∠ACD=90°,AC=CD
∴∠ECA+∠DCF=90°
又∵∠ECA+∠EAC=90°
∴∠DCF=∠EAC
在△ECA和△FDC中
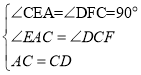
∴△ECA≌△FDC(AAS)
∴EC=DF,AE=CF
设直线AB的解析式为y=kx+b,将A、B代入可得:
![]()
解得![]()
∵直线AB的交y轴于点C
∴点C的坐标为:(0,![]() )
)
∴EC=yA-yC=![]() ,AE=xA=1,
,AE=xA=1,
∴DF=![]() ,CF=1,
,CF=1,
∴FO= yC-CF=![]()
故D点坐标为(![]() ,
,![]() ).
).
②若D点在第二象限,分别过点A、D作y轴的垂线交y轴于点E、F,如图所示
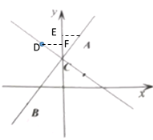
∵△ACD为等腰直角三角形
∴∠ACD=90°,AC=CD
∴∠ECA+∠DCF=90°
又∵∠ECA+∠EAC=90°
∴∠DCF=∠EAC
在△ECA和△FDC中
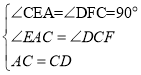
∴△ECA≌△FDC(AAS)
∴EC=DF,AE=CF
利用①中的结论
∴DF=![]() ,CF=1,
,CF=1,
∴FO= yC+CF=![]()
∵点D在第二象限
故D点坐标为(![]() ,
,![]() ).
).
综上所述:D点坐标为(![]() ,
,![]() )或(
)或(![]() ,
,![]() )
)

 阅读快车系列答案
阅读快车系列答案