��Ŀ����
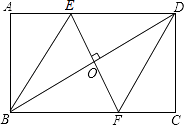
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У�������y=ax2+bx+c�ֱ�x����A��4��0����B����1��0������y���ڵ�C��0����3��������A��ֱ��y=�� ![]() x+3������������һ��D��
x+3������������һ��D��
��1���������ߵĽ���ʽ����D�����ꣻ
��2������Pλx���ϵ�һ�����㣬��Q���߶�AC�ϣ���Q��x��ľ���Ϊ ![]() ������PC��PQ������PCQ���ܳ���Сʱ�������P�����ꣻ
������PC��PQ������PCQ���ܳ���Сʱ�������P�����ꣻ
��3����ͼ2���ڣ�2���Ľ����£�����PD����ƽ�����Ƿ���ڡ�A1P1D1 �� ʹ��A1P1D1�ա�APD����A1��P1��D1�Ķ�Ӧ��ֱ���A��P��D��A1P1ƽ����y�ᣬ��P1�ڵ�A1�Ϸ������ҡ�A1P1D1����������ǡ�������������ϣ������ڣ��������A1�ĺ�����m���������ڣ���˵�����ɣ�
���𰸡�
��1��
�⣺�������߾���A��4��0����B����1��0����
�������ߵĽ���ʽΪy=a��x��4����x+1����
��C��0����3������y=a��x��4����x+1����
�ੁ3=��4a��
��a= ![]() ��
��
�������ߵĽ���ʽΪy= ![]() ��x��4����x+1��=
��x��4����x+1��= ![]() x2��
x2�� ![]() x��3��
x��3��
���� 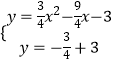 ��
��
��ã�x=��2��x=4����ȥ����
��x=��2����y=�� ![]() x+3��
x+3��
y= ![]() ��
��
��D����������2�� ![]() ����
����
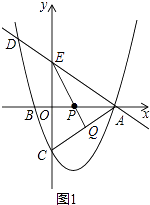
��2��
�⣺Ҫʹ��PCQ���ܳ���С��
��ֻ��ҪPC+PQ��С��
������֪��Q��x��ľ���Ϊ ![]() ��
��
����Q���������� ![]() ��
��
��ֱ��AC�Ľ���ʽΪy=k1x+b1��
��A��4��0����C��0����3������y=k1x+b1��
�� ![]() ��
��
��ã� 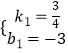 ��
��
��ֱ��AC�Ľ���ʽΪy= ![]() x��3��
x��3��
��y=�� ![]() ����y=
����y= ![]() x��3��
x��3��
��x= ![]() ��
��
��Q�������� ![]() ����
���� ![]() ����
����
��C����x��ԳƵĵ�ΪE����ͼ1��
��E��������0��3����
��ֱ��EQ�Ľ���ʽΪy=k2x+b2��
��Q�� ![]() ����
���� ![]() ����E��0��3������y=k2x+b2��
����E��0��3������y=k2x+b2��
�� 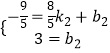 ��
��
�� ![]() ��
��
��ֱ��EQ�Ľ���ʽΪy=��3x+3��
��y=0����y=��3x+3��
��x=1��
��P������Ϊ��1��0��ʱ����PCQ���ܳ���С��
��3��
�⣺����D��DF��x���ڵ�F��
����D1��D1F1��A1P1����A1P1���ӳ����ڵ�F1��
�ߡ�A1P1D1�ա�APD��
��AF=A1F1=6��PF=P1F1=3��DF= ![]() ��
��
��A1��P1����������ʱ��
��A1P1��y�ᣬ
�����������ڣ�
��P1��D1����������ʱ��
��A1�ĺ�����Ϊm��
��P1��������m�� ![]() m2��
m2�� ![]() m��3����
m��3����
����D1��ֱ��A1P1���Ҳ�ʱ����ͼ2��
��ʱD�ĺ�����Ϊm+ ![]() ��
��
��x=m+ ![]() ����y=
����y= ![]() x2��
x2�� ![]() x��3��
x��3��
��D1��������m+ ![]() ��
�� ![]() m2+
m2+ ![]() m+
m+ ![]() ����
����
��F1��������m�� ![]() m2+
m2+ ![]() m+
m+ ![]() ����
����
��P1F1=�� ![]() m2+
m2+ ![]() m+
m+ ![]() ������
������ ![]() m2��
m2�� ![]() m��3��
m��3��
= ![]() m+
m+ ![]() ��
��
�� ![]() m+
m+ ![]() =3��
=3��
��m=�� ![]() ��
��
����D1��ֱ��A1P1�����ʱ����ͼ3��
��ʱD�ĺ�����Ϊm�� ![]() ��
��
��x=m�� ![]() ����y=
����y= ![]() x2��
x2�� ![]() x��3��
x��3��
��D1��������m+ ![]() ��
�� ![]() m2��9m+
m2��9m+ ![]() ����
����
��F1��������m�� ![]() m2��9m+
m2��9m+ ![]() ����
����
��P1F1=�� ![]() m2��9m+
m2��9m+ ![]() ������
������ ![]() m2��
m2�� ![]() m��3��
m��3��
=�� ![]() m+
m+ ![]() =3��
=3��
��m= ![]() ��
��
��A1��D1����������ʱ��
��A1�ĺ�����Ϊm��
��A1��������m�� ![]() m2��
m2�� ![]() m��3����
m��3����
����D1��ֱ��A1P1���Ҳ�ʱ����ͼ2��
��ʱD�ĺ�����Ϊm+ ![]() ��
��
��x=m+ ![]() ����y=
����y= ![]() x2��
x2�� ![]() x��3��
x��3��
��D1��������m+ ![]() ��
�� ![]() m2+
m2+ ![]() m+
m+ ![]() ����
����
��F1��������m�� ![]() m2+
m2+ ![]() m+
m+ ![]() ����
����
��A1F1=�� ![]() m2+
m2+ ![]() m+
m+ ![]() ������
������ ![]() m2��
m2�� ![]() m��3��
m��3��
= ![]() m+
m+ ![]() ��
��
�� ![]() m+
m+ ![]() =6��
=6��
��m= ![]() ��
��
����D1��ֱ��A1P1�����ʱ����ͼ3��
��ʱD�ĺ�����Ϊm�� ![]() ��
��
��x=m�� ![]() ����y=
����y= ![]() x2��
x2�� ![]() x��3��
x��3��
��D1��������m+ ![]() ��
�� ![]() m2��9m+
m2��9m+ ![]() ����
����
��F1��������m�� ![]() m2��9m+
m2��9m+ ![]() ����
����
��A1F1=�� ![]() m2��9m+
m2��9m+ ![]() ������
������ ![]() m2��
m2�� ![]() m��3��
m��3��
=�� ![]() m+
m+ ![]() =6��
=6��
��m=�� ![]() ��
��
������������m=�� ![]() ��
�� ![]() ��
�� ![]() ����
���� ![]() ʱ�����������⣮
ʱ�����������⣮
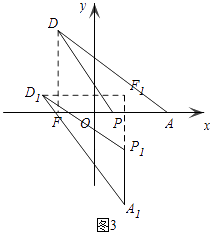
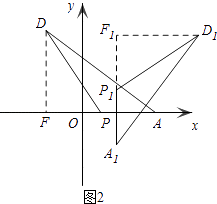
����������1����֪��������x�����������Ϊ��4��0���ͣ���1��0�������Կ��������ߵĽ���ʽΪy=a��x��4����x+1����Ȼ��ѣ�0��3���������ʽ������������ߵĽ���ʽ������ֱ�߽���ʽ�������߽���ʽ�������D�����ꣻ��2��Ҫ���PCQ����Сֵ�����ڵ�Q�ǹ̶��㣬����CQ�ǹ̶�����ģ����Ի���Ҫ���PC+PQ��̼��ɣ�������C����x��ĶԳƵ�E������EQ����x�ύ�ڵ�P����ʱP���ܹ�ʹ��PC+PQ��̣���3�������⻭��ͼ�ο�֪����D1��λ�������������һ����D1��ֱ��A1P1����ߣ���һ����D1��ֱ��A1P1���ұߣ������A1P1D1����������ǡ�������������������������һ��A1��P1���������ϣ�����P1��D1���������ϣ�����A1��D1���������ϣ�Ȼ����������ú�m��ʽ�ӱ�ʾA1��P1��D1�����������Ȼ������ȫ�������ε����ʼ������m��ֵ��
�����㾫����������������������Ľ������Ŀ�����жϼ��ɵõ��𰸣���Ҫ��֪һԪ���η��̵Ľ������Ӧ�Ķ��κ�����ͼ����x��Ľ������꣮���һԪ���η����е�b2-4ac���ڶ��κ����б�ʾͼ����x���Ƿ��н��㣮��b2-4ac>0ʱ��ͼ����x�����������㣻��b2-4ac=0ʱ��ͼ����x����һ�����㣻��b2-4ac<0ʱ��ͼ����x��û�н��㣮