题目内容
【题目】如图,在矩形ABCD中,边AB的长为3,点E,F分别在AD,BC上,连接BE,DF,EF,BD.若四边形BFDE是菱形,且OE=AE,则边BC的长为( ) 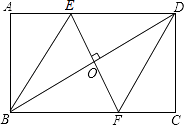
A.2 ![]()
B.3 ![]()
C.![]()
![]()
D.6 ![]()
【答案】B
【解析】解:
∵四边形ABCD是矩形,
∴∠A=90°,∠ABC=90°,AB=CD,
即EA⊥AB,
∵四边形BFDE是菱形,
∴BD⊥EF,
∵OE=AE,
∴点E在∠ABD的角平分线上,
∴∠ABE=∠EBD,
∵四边形BFDE是菱形,
∴∠EBD=∠DBC,
∴∠ABE=∠EBD=∠DBC=30°,
∵AB的长为3,
∴BC=3 ![]() ,
,
故选B.
【考点精析】认真审题,首先需要了解菱形的性质(菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半),还要掌握矩形的性质(矩形的四个角都是直角,矩形的对角线相等)的相关知识才是答题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目